Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 700-710
Об устойчивости равновесия плазмы в окрестности прямого проводника с током
К. В. Брушлинский 1, 2, С. А. Кривцов 2, Е. В. Степин 1, 2, *
1 Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия
2 Национальный исследовательский ядерный университет “МИФИ”
115409 Москва, Каширское ш., 31, Россия
* E-mail: eugene.v.stepin@gmail.com
Поступила в редакцию 14.11.2019
После доработки 14.11.2019
Принята к публикации 16.12.2019
Аннотация
Представлена математическая модель равновесной магнитоплазменной конфигурации в плазменном цилиндре, вдоль оси которого расположен проводник конечного диаметра с током, создающим удерживающее плазму магнитное поле. Рассматриваемые здесь конфигурации кольцевой формы – простейший элемент широкого класса ловушек-галатей с погруженными в плазменный объем проводниками. Задачи о таких конфигурациях имеют простое аналитическое решение в терминах обыкновенных дифференциальных уравнений. Получен простой результат о существовании гладких равновесных конфигураций при ограничении максимального давления плазмы, отнесенного к магнитным единицам. Поставлены и решены задачи об устойчивости конфигураций – полномасштабной МГД-устойчивости и промежуточной устойчивости относительно возмущений той же размерности. Показано, что промежуточная устойчивость имеет место в пределах указанного ограничения давления, а МГД-устойчивость усиливает это ограничение за счет гофрированных возмущений, зависящих от осевой координаты. Библ. 27. Фиг. 5.
ВВЕДЕНИЕ
Статья относится к циклу работ по математическому моделированию и расчетам равновесных плазменных конфигураций, удерживаемых магнитным полем ловушек, представляющих интерес в заманчивых перспективах управляемого термоядерного синтеза. Более конкретно речь идет о ловушках, в которых проводники с током, создающие магнитное поле, погружены в плазменный объем, что делает геометрию поля более сложной и разнообразной и позволяет рассчитывать на более эффективное удержание. Дополнительную сложность исследований конфигураций создает существенное требование, чтобы проводники в них не соприкасались с горячей плазмой. Внимание к этому классу ловушек привлечено А.И. Морозовым, назвавшим их “галатеями” [1]. Согласно основному замыслу, они имеют тороидальную форму вроде токамака с погруженными в него кольцевыми проводниками. Однако для простоты исследований основные положения, касающиеся конфигураций, как правило, ведутся в их распрямленных в цилиндр аналогах (торах бесконечного радиуса) с прямыми или винтовыми проводниками. Первым примером галатей, обсуждавшимся в литературе, была “стелларатор-галатея” (СГ). Ее идея предложена в [2], а численная модель в распрямленном в цилиндр варианте с тремя винтовыми проводниками реализована в [3]. Здесь в расчетах получено ограничение на величину давления плазмы, измеренную в магнитных единицах, которое теоретически обосновано в [4]. В расчетах конфигураций СГ с плазмой, сосредоточенной на сепаратрисе магнитного поля, установлено, что здесь это ограничение слабее, чем в конфигурациях с плазмой на оси, что говорит о более эффективном удержании в галатее по сравнению с традиционными стеллараторами [5].
Много внимания уделено ловушке “Галатея-Пояс” с двумя кольцевыми проводниками в плазменном торе и ее цилиндрическому аналогу с прямыми проводниками. Предложенная в [6], она стала предметом исследований теоретических [6], [7], экспериментальных [8], [9] и численных [10], [11]. Обращено внимание на ее аналогию с токовым слоем С.И. Сыроватского [12] и также на отличие от него [13]. В расчетах “Пояса” также получено ограничение на допустимое отношение газового и магнитного давлений (“плазменное $\beta $”). Содержательный обзор работ 1990-х годов по галатеям имеется в статье А.И. Морозова и В.В. Савельева [14].
Математические модели равновесных конфигураций в предположении плоской, осевой или винтовой симметрии построены в терминах двумерных краевых задач с полулинейным эллиптическим дифференциальным уравнением Грэда–Шафранова [15], [16] для скалярной функции магнитного потока. Задачи решаются численно итерационным методом установления по времени. Проведен также расчет формирования равновесной конфигурации в цилиндрическом аналоге “Пояса” в двумерной нестационарной МГД-модели [17].
Установление равновесных конфигураций в обоих случаях позволяет говорить об их устойчивости в некотором ограниченном смысле, а именно, устойчивости относительно малых возмущений той же неполной размерности, что и невозмущенные решения задачи. Эта условная устойчивость, очевидно, необходима для полноценной МГД-устойчивости относительно трехмерных возмущений, но не достаточна. Тем не менее она может представить интерес в качестве “промежуточного этапа” исследования устойчивости. Сходимость итераций в решении краевых задач с уравнением Грэда–Шафранова названа “диффузионной устойчивостью”, и показано, что если она имеет место для всех конфигураций в цилиндре с винтовым магнитным полем, то такие конфигурации МГД-устойчивы [18]–[20]. Особенности равновесных конфигураций и некоторые вопросы их устойчивости удобно рассмотреть на примере одномерных задач в кольцевой окрестности одного прямого проводника, которые можно считать простейшей моделью основного элемента любой ловушки-галатеи. Такой подход был впервые реализован в [21] в частном случае постоянного тока в плазме, параллельного току в проводнике. Равновесные конфигурации в этом случае не соответствуют сформулированным выше требованиям, так как плазма в них прижата к проводнику. Изолированную от проводника конфигурацию удалось получить в нестационарной МГД-модели при возрастании тока в проводнике со временем на начальном этапе формирования. Эта идея озвучена в двумерной МГД-модели формирования равновесия в цилиндрическом аналоге “Галатеи-Пояса” [22].
В настоящей работе равновесные значения давления плазмы, осевого тока и азимутального поля выбраны так, чтобы давление обращалось в нуль на границе кольца (проводнике и внешнем кожухе) и было максимальным посредине на конечном расстоянии от них. Аналитическое решение задачи о равновесии и здесь существует при ограничении на безразмерное значение максимума давления ${{p}_{0}} < p_{0}^{{{\text{cr}}}}$. В попытках превысить $p_{0}^{{{\text{cr}}}}$ давление приходится “обрезать”, т.е. положить постоянным в средней части кольца, в которой магнитное поле и электрический ток отсутствуют, что напоминает “фигуры равновесия”, исследованные в [14], [23], [24]. Авторам показалось интересным получить те же конфигурации независимо с помощью численного решения одномерного аналога уравнения Грэда–Шафранова. Оказалось, что при ${{p}_{0}} < p_{0}^{{{\text{cr}}}}$ итерационный метод установления сходится, т.е. в пределах указанного ограничения решение условно устойчиво в этом смысле. Параллельно проведено исследование МГД-устойчивости относительно трехмерных возмущений в линейном приближении. Установлено, что при том же ограничении ${{p}_{0}} < p_{0}^{{{\text{cr}}}}$ конфигурации теряют устойчивость при внесении гофрированных возмущений, зависящих от $z$.
При ${{p}_{0}} > p_{0}^{{{\text{cr}}}}$ итерации не сходятся, однако это может быть следствием разрыва некоторых элементов равновесного решения, который не совместился с “гладкой” природой уравнения Грэда–Шафранова. Однако сама необходимость менять модель конфигурации, создавая внутри нее указанную выше область постоянного давления без поля и тока, указывает на очередную разновидность ограничения максимального давления. Физический смысл ограничения очевиден: ловушка с заданными электромагнитными параметрами может удержать плазму лишь ограниченного давления.
1. ПОСТАНОВКА ЗАДАЧИ. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
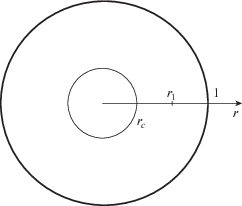
Объектом исследования являются равновесные конфигурации плазмы, магнитного поля и электрического тока в бесконечном круглом цилиндре, вдоль оси которого расположен круглый проводник конечного диаметра с постоянным током, создающим азимутальное магнитное поле. Кольцевая область сечения этой конструкции плоскостью $z = {\text{const}}$ изображена на фиг. 1. Находящаяся в ней плазма допускает приближение сплошной среды и описывается уравнениями плазмостатики:
(1.1)
$\nabla p = {\mathbf{j}} \times {\mathbf{H}};\quad {\mathbf{j}} = \operatorname{rot} {\mathbf{H}};\quad \operatorname{div} {\mathbf{H}} = 0,$Конфигурации можно считать симметричными, в данном случае одномерными, то есть в цилиндрических координатах ($r$, $\varphi $, $z$) будем иметь
(1.2)
$\frac{\partial }{{\partial \varphi }} \equiv 0;\quad \frac{\partial }{{\partial z}} \equiv 0;\quad {\mathbf{H}} = (0,H,0);\quad {\mathbf{j}} = (0,0,j).$Уравнения (1.1) при этом превращаются в систему двух обыкновенных дифференциальных уравнений:
поскольку третье уравнение (1.1) выполнено автоматически в силу (1.2). Уравнения (1.1) и (1.3) написаны в безразмерных переменных. Единицы всех величин составлены из двух размерных констант, заданных при постановке задачи – радиуса $R$ внешнего цилиндра и величины электрического тока $J$ в проводнике, а именно:(1.4)
${{r}_{{\text{u}}}} = R;\quad {{H}_{{\text{u}}}} = \frac{{2J}}{{cR}};\quad {{j}_{{\text{u}}}} = \frac{c}{{4\pi }}\frac{{{{H}_{{\text{u}}}}}}{R};\quad {{p}_{{\text{u}}}} = \frac{{H_{{\text{u}}}^{2}}}{{4\pi }},$Задача с уравнениями (1.3) ставится на отрезке
где ${{r}_{c}}$ – безразмерное значение радиуса проводника.Три скалярных функции $p$, $H$, $j$ должны удовлетворять двум уравнениям (1.3). Следовательно, эти уравнения определяют искомые конфигурации с точностью до одной произвольной функции, выбор которой должен соответствовать требованиям или пожеланиям к окончательному решению. Основное требование здесь – изолировать плазму от проводника и внешней границы, т.е. от обоих концов отрезка (1.5). Были испробованы разные способы задания $H(r)$ и $j(r)$ с целью обратить положительную функцию $p(r)$ в нуль на концах, однако удобнее сразу задавать $p(r)$, например, в виде параболы:
(1.6)
$p(r) = {{p}_{0}}\left( {1 - \frac{{{{{(r - {{r}_{1}})}}^{2}}}}{{{{{(1 - {{r}_{1}})}}^{2}}}}} \right),\quad {{r}_{1}} = \frac{{{{r}_{c}} + 1}}{2},$Два уравнения (1.3) требуют задания двух дополнительных условий. В качестве одного из них задается значение
соответствующее циркуляции магнитного поля, окружающего заданный ток $J$. Роль второго условия сыграл выбор $p(r)$, из которого следует второе граничное условие, например, в виде значения $H(1)$, однозначно определяемого с помощью (1.3) и (1.6). Физический смысл $H(1)$ – циркуляция магнитного поля вокруг всего цилиндра, которая соответствует значению полного тока в круге $r < 1$, т.е. сумме тока $J$ в проводнике и плазменного тока, протекающего в рассматриваемой кольцевой области (1.5).Решая уравнения (1.3) с заданным $p(r)$ согласно (1.6) и граничному условиию (1.7), получаем
(1.8)
$G(r) \equiv {{(Hr)}^{2}} = 1 - \int\limits_{{{r}_{c}}}^r {2{{r}^{2}}\frac{{dp}}{{dr}}} dr = 1 + \frac{{4{{p}_{0}}}}{{{{{(1 - {{r}_{1}})}}^{2}}}}\left( {\frac{{{{r}^{4}} - r_{c}^{4}}}{4} - {{r}_{1}}\frac{{{{r}^{3}} - r_{c}^{3}}}{3}} \right),$Решение в виде (1.8), (1.9), очевидно, существует лишь при $G(r) \geqslant 0$, откуда следует упомянутое во введении ограничение ${{p}_{0}} < p_{0}^{{{\text{cr}}}}$, где $p_{0}^{{{\text{cr}}}}$ определяется равенствами
(1.10)
$\mathop {{\text{min}}}\limits_r G(r) = G({{r}_{1}}) = 0,\quad ~{\text{т}}{\text{.е}}{\text{.}}\quad p_{0}^{{{\text{cr}}}} = \frac{{{{{(1 - {{r}_{1}})}}^{2}}}}{4}{{\left( {{{r}_{1}}\frac{{{{r}_{1}}^{3} - r_{c}^{3}}}{3} - \frac{{{{r}_{1}}^{4} - r_{c}^{4}}}{4}} \right)}^{{ - 1}}}.$Представленные ниже решения задачи получены для кольца (1.5) с радиусом проводника ${{r}_{c}} = 0.2$. Ему соответствует критическое значение $p_{0}^{{{\text{cr}}}} \approx 4.17$. На фиг. 2 и 3 представлены графики всех трех искомых функций для двух докритических значений ${{p}_{0}} = 1$ и ${{p}_{0}} = 4$, то есть одного – далекого от $p_{0}^{{{\text{cr}}}}$, другого – близкого к нему. Следует заметить, что давление ${{p}_{0}}$ определяет граничное значение $Hr = H(1)$ на внешней границе, которое в выбранных единицах соответствует величине полного тока в кольце, включая проводник. Таким образом, плазменный ток в кольце равен
Фиг. 2.
Равновесное распределение давления $p$, магнитного поля $H$ и электрического тока $j$ в окрестности проводника при ${{p}_{0}} = 1$.

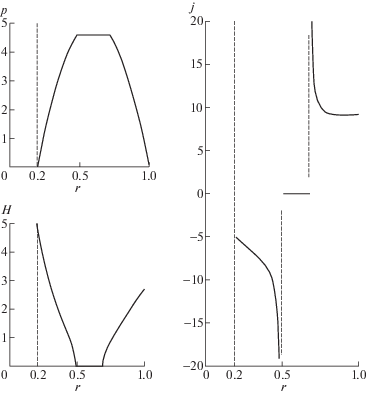
Фиг. 3.
Равновесное распределение давления $p$, магнитного поля $H$ и электрического тока $j$ в окрестности проводника при ${{p}_{0}} = 4$.

При ${{p}_{0}} = 1$ его безразмерное значение ${{J}^{{{\text{pl}}}}} \approx 0.5$, т.е. равно половине тока в проводнике, а при ${{p}_{0}} = 4$ превосходит его: ${{J}^{{{\text{pl}}}}} \approx 1.5$, т.е. плазменный ток заметно возрастает вместе с давлением.
Плотность плазменного тока $j(r)$ отрицательна при $r < {{r}_{1}}$ и положительна при $r > {{r}_{1}}$. Отрицательный, т.е. противоположный по направлению току в проводнике, он в части кольца, примыкающей к проводнику, обеспечивает изоляцию последнего от плазмы с помощью амперовой силы ${\mathbf{j}} \times {\mathbf{H}} = \nabla p$, сонаправленной с градиентом давления. Та же сила при положительном токе $j(r)$ не позволяет плазме прикасаться к внешней границе $r = 1$. Необходимость в отрицательном токе у проводника отмечена в работе [22] в нестационарной задаче о формировании “Галатеи-Пояса” и подтверждена в расчетах равновесия и его формирования в последующей литературе [10], [17], [19]. Абсолютная величина тока $j(r)$ в рассмотренных конфигурациях у внешней границы больше, чем у внутренней, и возрастает вместе с давлением, что и отмечено выше в обсуждении полного плазменного тока. По мере приближения ${{p}_{0}}$ к $p_{0}^{{{\text{cr}}}}$ графики $j(r)$ становятся круче при $r \sim {{r}_{1}}$, т.е. в области максимального давления.
При ${{p}_{0}} > p_{0}^{{{\text{cr}}}}$ значения $G(r)$ в формуле (1.8) становятся отрицательными при $r > {{r}_{2}}$, где $G({{r}_{2}}) = 0$, ${{r}_{2}} < {{r}_{1}}$, и не пригодны для решения задачи. Чтобы продолжить решение, можно “срезать” параболу (1.6), заменив ее постоянным значением $p \equiv p({{r}_{2}})$ при $r > {{r}_{2}}$ и восстановить ее при ${{r}_{3}} = 2{{r}_{1}} - {{r}_{2}}$ – значении, симметричном ${{r}_{2}}$ относительно ${{r}_{1}}$, чтобы использовать ту же параболу при $r > {{r}_{3}}$. В интервале ${{r}_{2}} < r < {{r}_{3}}$ полагаем
При $r \geqslant {{r}_{3}}$ из уравнения (1.3) следует
(1.11)
$G(r) = - \int\limits_{{{r}_{3}}}^r {2{{r}^{2}}} \frac{{dp}}{{dr}}dr = \frac{{4{{p}_{0}}}}{{{{{(1 - {{r}_{1}})}}^{2}}}}\left( {\frac{{{{r}^{4}} - r_{3}^{4}}}{4} - {{r}_{1}}\frac{{{{r}^{3}} - r_{3}^{3}}}{3}} \right),$Графики $p$, $H$ и $j$ при ${{p}_{0}} = 5$ представлены на фиг. 4. Они напоминают “фигуры равновесия” с постоянным давлением плазмы без электрического тока и магнитного поля, окруженные вакуумом с магнитным полем, которое создается “скинированным” током, текущим только по поверхности. Такие фигуры исследованы А.И. Морозовым и В.В. Савельевым с применением теории аналитических функций комплексной переменной [14], [19], [23], [24].
2. ВОПРОСЫ УСТОЙЧИВОСТИ РАВНОВЕСНЫХ ПЛАЗМЕННЫХ КОНФИГУРАЦИЙ
Удержание плазмы магнитным полем в ловушках требует устойчивого существования обсуждаемых равновесных конфигураций. Проблема их устойчивости постоянно присутствует в современной научной литературе, посвященной разнообразным проявлениям плазменных неустойчивостей и попыткам борьбы с ними. Строго говоря, устойчивость должна быть исследована хотя бы в линейном приближении относительно любых малых возмущений МГД-переменных, трехмерных, независимо от имеющейся симметрии невозмущенной конфигурации. Симметрия вносит упрощение в коэффициенты линейных уравнений, позволяет расчленить трехмерную задачу на серию более простых для отдельных гармоник возмущений. Для одномерных равновесий в цилиндре этому вопросу посвящены, например, обзоры [25], [26], статья [18] и уделено внимание в книгах [19], [20].
В то же время численные модели равновесия в симметричных ловушках, в том числе галатеях, получены в терминах решения двумерных краевых задач с одним скалярным уравнением Грэда–Шафранова для функции магнитного потока, к которому сводятся уравнения плазмостатики (1.1) [15], [16]. В задачах о равновесии конфигураций с плоской симметрией (${\partial \mathord{\left/ {\vphantom {\partial {\partial z \equiv 0}}} \right. \kern-0em} {\partial z \equiv 0}}$), например, в цилиндре, оно имеет вид (в безразмерных переменных, как и выше)
(2.1)
$\Delta \psi + \frac{{dp}}{{d\psi }} + I\frac{{dI}}{{d\psi }} + {{j}^{{{\text{ex}}}}}(r,\varphi ) = 0.$Последнее слагаемое в уравнении моделирует заданный ток в проводниках и сосредоточено в местах их пересечения с плоскостью $z = {\text{const}}$. Давление плазмы $p$ и функция $I$ электрического тока в плоскости сечения цилиндра зависят от $\psi $, т.е. постоянны на магнитных поверхностях (линиях в плоскости сечения цилиндра) $\psi = {\text{const}}$. Они должны быть заданы в соответствии с особенностями конкретной задачи. В галатеях с цилиндрической геометрией достаточно положить ${{H}_{z}} = I(\psi ) \equiv 0$, а зависимость $p(\psi )$ выбрать так, чтобы расположить плазму на линиях $\psi = {\text{const}}$ вдали от проводников и внешней границы. Краевая задача с уравнением (2.1) ставится в сечении ловушки с границей $\Gamma $, непрозрачной для магнитного поля: ${{\left. \psi \right|}_{\Gamma }} = 0$, и численно решается итерационным методом установления. Решение задач этого класса содержит один общий результат: итерационный процесс сходится только при ограничении сверху на характерную величину безразмерного давления. Физический смысл его упомянут выше, но результат имеет и математическую природу, которая не зависит от численных методов решения. Сходимость итераций требует убывания “со временем” погрешности $u(t,r,\varphi )$, что обеспечивается положительной определенностью оператора линеаризованного уравнения
Здесь суть младшие члены уравнения (2.1) для невозмущенного решения $\psi (r,\varphi )$.Этот общий результат, помимо плазмостатики, относится к более широкому классу задач о взаимодействии процессов реакции и диффузии, например, в теории горения, использующих математический аппарат полулинейного уравнения типа (2.1) любой размерности (см. [19] с соответствующей библиографией).
Сходимость итераций можно истолковать как некоторую устойчивость решения, но только относительно возмущений участвующих в задаче величин ограниченной размерности. Такая устойчивость, названная “диффузионной” [18], необходима, но не достаточна для МГД-устойчивости плазмы в общепринятом смысле. Тем не менее она может представлять интерес, неся в себе некоторую промежуточную количественную информацию о процессах, способствующих или препятствующих устойчивости. “Диффузионная” устойчивость равносильна положительному спектру дифференциального оператора (2.2), который, в свою очередь, зависит от коэффициента $Q(\psi )$. Оператор $ - \Delta \psi $ положителен практически в любой геометрии. Хорошо известно (см., например, [27]), что при
спектр $L$ смещен вправо и, следовательно, становится “еще более положительным”, т.е. задача устойчива.Если условие (2.3) не выполнено, но коэффициент $Q(\psi )$ ограничен сверху положительной константой
то его спектр можно сравнивать со спектром оператора $ - \Delta \psi $, а именно, записав $L[u] = \lambda u$ в виде Здесь коэффициент при $u$ неотрицателен, следовательно, собственные значения оператора в левой части равенства удовлетворяют неравенству где $\mu $ – положительные собственные значения оператора $ - \Delta u$.Отсюда следует достаточное условие
положительности оператора $L[u]$ и диффузионной устойчивости рассматриваемой конфигурации. Здесь ${{\mu }_{1}}$ – первое, т.е. минимальное собственное значение $ - \Delta u$, которое во многих простых вариантах геометрии может быть легко вычислено.Таким образом, вопрос о диффузионной устойчивости решения задачи требует численного решения задачи с уравнением (2.1), только если ${{Q}_{{\max }}} > {{\mu }_{1}}$. Рассмотрим промежуточную устойчивость полученных в разд. 1 одномерных конфигураций в кольцевой окрестности проводника с током. Для этого попытаемся воспроизвести их с помощью уравнения Грэда–Шафранова. Его одномерный вариант для функции $\psi $, связанной с магнитным полем уравнением $H = - {{d\psi } \mathord{\left/ {\vphantom {{d\psi } {dr}}} \right. \kern-0em} {dr}}$, имеет вид
(2.5)
$\frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d\psi }}{{dr}}} \right) + \frac{{dp}}{{d\psi }} = 0.$В итерационном процессе нелинейное слагаемое в (2.5) берется с предыдущего слоя (итерации). Итерационный процесс установления состоит в численном решении методом прогонки разностного аналога уравнения (2.5), дополненного производной по времени ${{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial t}}} \right. \kern-0em} {\partial t}}$:
В качестве нулевого приближения удобно взять любую монотонно убывающую функцию $\psi (r)$, например, линейную.
В расчетах, проведенных этим методом, получены установившиеся равновесные значения функции $\psi (r)$. Они представлены на фиг. 5. Определенные с ее помощью $H$, $j$ и $p$ совпали с изложенными в разд. 1 результатами при всех значениях параметра ${{p}_{0}} < p_{0}^{{{\text{cr}}}}$, т.е. ограничение давления с помощью очевидного требования $(H{{r}^{2}}) \geqslant 0$ оказалось сильнее требования обсуждаемой промежуточной устойчивости. Этот же результат следует из условия (2.4) при ${{p}_{0}} < p_{0}^{{{\text{cr}}}}$, где ${{Q}_{{\max }}} < {{\mu }_{1}}$, а ${{\mu }_{1}} \approx 6.5$ (вычисляется с помощью корней бесселевых функций ${{J}_{0}}(x)$ и ${{J}_{1}}(x)$). При ${{p}_{0}} > p_{0}^{{{\text{cr}}}}$ итерационный процесс решения задачи с уравнением (2.1) расходится, однако считать “обрезанные” решения на фиг. 4 неустойчивыми, по-видимому, преждевременно, т.к. разрывы функции $j(r)$ и производных функций $H(r)$ и $p(r)$ могут оказать влияние на решение эллиптического уравнения, обычно имеющего дело с гладкими функциями.
Таким образом, в данном случае можно ограничиться выводом, что промежуточная устойчивость конфигураций с заданным давлением (1.6) и само существование гладких решений задачи ограничены одним и тем же пределом $p_{0}^{{{\text{cr}}}}$, определяемым формулой (1.10).
3. МГД-УСТОЙЧИВОСТЬ
Необходимость, но не достаточность рассмотренной диффузионной устойчивости подтверждается примером расчета МГД-устойчивости конфигураций в кольце для нескольких гармоник малых линейных возмущений. В линейных однородных уравнениях для трехмерных возмущений коэффициенты составлены из равновесного решения, поэтому не зависят от переменных $t$, $\varphi $, $z$, следовательно, их частные решения зависят от этих переменных экспоненциально посредством множителя
с действительными значениями $k$ и целыми значениями $m$. В результате семь уравнений для возмущений векторов скорости ${{{\mathbf{V}}}_{1}}$ и магнитного поля ${{{\mathbf{H}}}_{1}}$ и скаляра ${{p}_{1}}$ после громоздких выкладок приводят к задачам на собственные значения с уравнением второго порядка для функции $u = {{V}_{{1r}}}r$:(3.2)
$ - \frac{1}{r}\frac{d}{{dr}}\left( {r{{F}_{{m,k}}}\frac{{du}}{{dr}}} \right) + {{G}_{{m,k}}}u = 0,$Численно решая его с начальными условиями $u({{r}_{c}}) = 0$, $u{\text{'}}({{r}_{c}}) > 0$ и разными значениями параметра ${{p}_{0}}$, подбираем “методом стрельбы” такое его значение, при котором $u(1)$ обратится в нуль.
Первые расчеты проведены для $m = 1$, т.е. для первой гармоники по $\varphi $ и разных значениях показателя $k$ в формуле (3.2), который характеризует зависимость возмущений от координаты $z$.
В расчетах установлены следующие результаты. Гармоники с $k = 0,1,2$ оказались устойчивыми во всем диапазоне ${{p}_{0}} < p_{0}^{{{\text{cr}}}} \approx 4.17$. При $k = 3$ собственная функция с $\omega = 0$ появилась при ${{p}_{0}} = 3.17$. Это значит, что конфигурация устойчива относительно данной гармоники возмущений при ${{p}_{0}} < 3.17$. С ростом частоты $k$ диапазон значений ${{p}_{0}}$ сужается, т.е. пороговые значения ${{p}_{0}}$ убывают: при $k = 5$ до ${{p}_{0}} = 1.34$, при $k = 10$ до ${{p}_{0}} = 0.55$.
Таким образом, рассмотренные конфигурации в кольце устойчивы относительно независимых от $z$ возмущений в пределах ${{p}_{0}} < p_{0}^{{{\text{cr}}}} \approx 4.17$ и становятся все менее устойчивыми, если включить их “гофрированную” зависимость от $z$. Неустойчивость усиливается при возрастании частоты $k$ колебаний по $z$.
Этот результат качественно повторяет хорошо известные результаты о неустойчивости Z-пинча (того же цилиндра, но без проводника внутри) [11], [19], [25].
ЗАКЛЮЧЕНИЕ
Рассмотрены вопросы устойчивости равновесных конфигураций плазмы, магнитного поля и электрического тока в цилиндрической окрестности кольцевого сечения вокруг прямого проводника с током. В простейшей одномерной модели получены явные выражения для характеристик конфигураций и установлено ограничение на отношение газового и магнитного давлений, в пределах которого могут существовать равновесные конфигурации, не соприкасающиеся с проводником. Проведено два этапа исследования устойчивости конфигураций. Они оказались устойчивыми относительно возмущений ограниченной размерности, но диапазон устойчивых значений давления сужается при включении возмущений, зависящих от координаты $z$.
Список литературы
Морозов А.И. О галатеях – плазменных ловушках с омываемыми плазмой проводниками // Физ. плазмы. 1992. Т. 18. Вып. 3. С. 305–316.
Морозов А.И., Пустовитов В.Д. О стеллараторе с левитирующими обмотками // Физ. плазмы. 1991. Т. 17. Вып. 10. С. 1276.
Брушлинский К.В., Зуева Н.М., Михайлова М.С., Морозов А.И., Пустовитов В.Д., Тузова Н.Б. Численное моделирование прямых винтовых шнуров с проводниками, погруженными в плазму // Физ. плазмы. 1994. Т. 20. № 3. С. 284–292.
Брушлинский К.В., Зуева Н.М., Михайлова М.С., Петровская Н.Б. О единственности и устойчивости решений двумерных задач плазмостатики // Матем. моделирование. 1995. Т. 7. № 4. С. 73–86.
Брушлинский К.В., Морозов А.И., Петровская Н.Б. Численное моделирование винтовой равновесной конфигурации с плазмой на сепаратрисе // Матем. моделирование. 1998. Т. 10. № 11. С. 29–36.
Морозов А.И., Франк А.Г. Тороидальная магнитная ловушка-галатея с азимутальным током // Физ. плазмы. 1994. Т. 20. № 11. С. 982–989.
Морозов А.И., Мурзина М.В. Простейшие равновесные конфигурации галатей типа “Пояс” // Физ. плазмы. 1996. Т. 22. № 6. С. 551–563.
Богданов С.Ю., Марков В.С., Морозов А.И., Франк А.Г. Плазменная конфигурация “Галатея-Пояс”. Первые результаты экспериментальных исследований // Письма в ЖЭТФ. 1995. Т. 21. Вып. 24. С. 5–9.
Франк А.Г., Кирий Н.П., Марков В.С. Эксперименты по формированию магнитоплазменных конфигураций “Галатея-пояс” // Физ. плазмы. 2019. Т. 45. № 1. С. 32–36.
Брушлинский К.В., Гольдич А.С., Десятова А.С. Плазмостатические модели магнитных ловушек-галатей // Матем. моделирование. 2012. Т. 24. № 8. С. 81–86.
Брушлинский К.В., Кондратьев И.А. Сравнительный анализ расчетов равновесия плазмы в тороидальных и цилиндрических магнитных ловушках // Матем. моделирование. 2018. Т. 30. № 6. С. 76–94.
Сыроватский С.И. Токовые слои и вспышки в космической и лабораторной плазме // Вестник АН СССР. 1977. № 10. С. 33–44.
Брушлинский К.В., Гольдич А.С., Давыдова Н.А. Плазменные конфигурации в ловушках-галатеях и токовых слоях // Матем. моделирование. 2016. Т. 28. № 7. С. 107–120.
Морозов А.И., Савельев В.В. О галатеях – ловушках с погруженными в плазму проводниками // Успехи физ. наук. 1998. Т. 168. № 11. С. 1153–1194.
Шафранов В.Д. О равновесных магнитогидродинамических конфигурациях // ЖЭТФ. 1957. Т. 33. Вып. 3 (9). С. 710–722.
Grad H., Rubin H. Hydrodynamic equilibria and force-free fields // Proc. 2nd United Nations Int. Conf. on the Peaceful Uses of Atomic Energy. Geneva. 1958. V. 31. P. 190–197 / N.Y. Columbia Univ. Press. 1959.
Брушлинский К.В., Чмыхова Н.А. Численная модель формирования квазиравновесия плазмы в магнитном поле ловушек-галатей // Вестник НИЯУ МИФИ. 2014. Т. 3. № 1. С. 40–52.
Брушлинский К.В. Два подхода к задаче об устойчивости равновесия плазмы в цилиндре // Прикл. матем. и механ. 2001. Т. 65. Вып. 2. С. 235–243.
Брушлинский К.В. Математические и вычислительные задачи магнитной газодинамики. М.: БИНОМ. Лаборатория знаний, 2009. 200 с.
Брушлинский К.В. Математические основы вычислительной механики жидкости, газа и плазмы. Долгопрудный: Изд. дом “Интеллект”, 2017. 272 с.
Брушлинский К.В., Чмыхова Н.А. О равновесии плазмы в магнитном поле ловушек-галатей // Матем. моделирование. 2010. Т. 22. № 6. С. 3–14.
Дудникова Г.И., Морозов А.И., Федорук М.П. Численное моделирование прямых плазменных конфигураций – галатей типа “Пояс” // Физ. плазмы. 1997. Т. 23. № 5. С. 387–396.
Морозов А.И., Савельев В.В. Фигуры равновесия идеальной плазмы с $\beta = 1$ в магнитном поле // Физ. плазмы. 1993. Т. 19. № 8. С. 977–989.
Савельев В.В. Фигуры равновесия идеальной плазмы с током в магнитном поле // Физ. плазмы. 1995. № 3. С. 216–220.
Кадомцев Б.Б. Гидромагнитная устойчивость плазмы // Вопросы теории плазмы / Ред. М.А. Леонтович. М.: Госатомиздат, 1963. Вып. 2. С. 132–176.
Соловьев Л.С. Симметричные магнитогидродинамические течения и винтовые волны в круглом плазменном цилиндре // Вопросы теории плазмы / Ред. М.А. Леонтович. М.: Госатомиздат, 1963. Вып. 3. С. 245–289.
Арсенин В.Я. Методы математической физики и специальные функции. М.: Наука, 1984. 384 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики