Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 711-724

ВВЕДЕНИЕ

Согласно модели “Зельдовича–Неймана–Дёринга” (ЗНД-модели) [1]–[3] структура детонационной волны (ДВ) включает ударную волну (поверхность разрыва) и примыкающую к ней “зону реакций” конечной ширины. Действительная толщина ударной волны – несколько длин свободного пробега при многократно более протяженной зоне реакций. Химические реакции, скорость которых сильно зависит от температуры, начинаются из-за нагрева горючей смеси ударной волной и заканчиваются достижением продуктами сгорания термодинамического равновесия. Получающиеся в рамках ЗНД-модели детонационные адиабаты полностью определяются термодинамикой смеси в исходном (холодном, метастабильном) и в конечных равновесных состояниях, не завися от кинетики горения. На детонационных адиабатах особо интересны точки, которые отвечают ДВ, названным по именам их первооткрывателей [4], [5] ДВ Чепмена–Жуге (ДВ_CJ). Важная особенность ДВ_CJ – равная звуковой нормальная к ДВ компонента скорости газа за ней [6]–[8]. По этой причине ДВ_CJ оказывается “самоподдерживающейся”, ибо волны разрежения, идущие от “центра взрыва” (места инициирования ДВ начальным выделением энергии или ударной волной вблизи затупления обтекаемого сверхзвуковым потоком тела), не могут ее догнать и ослабить.

Экспериментально обнаруженные в середине ХХ века случаи развала ожидаемых в рамках ЗНД-модели стационарных структур ДВ вызвали поток исследований их “структурной” устойчивости. В работах этого направления реальная кинетика заменялась одной реакцией с некоторой “энергией активации” и последующим мгновенным или протяженным по времени тепловыделением. В таком приближении условие структурной устойчивости приводит к ограничениям на энергию активации. В настоящее время выяснение одномерной структурной устойчивости ДВ в любой смеси при известной кинетике горения возможно в процессе численного решения сравнительно простой нестационарной задачи о неравновесном одномерном течении идеального газа. Если решение такой задачи выходит на стационарную структуру, то ДВ в данной смеси структурно устойчива. В противном случае ДВ структурно неустойчива.

Наряду со структурной устойчивостью ДВ представляет интерес устойчивость стационарных течений в каналах переменной площади со структурно устойчивой и поэтому рассматриваемой как поверхность разрыва ДВ. Интерес к таким течениям – следствие их предполагаемого использования в качестве элемента прямоточных двигателей с горением в стационарных ДВ обычно – ДВ_CJ [9]–[12]. На первый взгляд, выбор в качестве стационарной именно ДВ_CJ представляется естественным, ведь она самоподдерживающаяся. Однако одно дело выход на ДВ_CJ первоначально пересжатой ДВ при удалении от источника инициирования, а совсем другое – прямая ДВ, стоящая в канале переменной площади F = F(x). Как установлено в [13], все одномерные стационарные течения с ДВ_CJ неустойчивы. Остается выяснить, устойчивы ли подобные стационарные течения с пересжатой ДВ. Разработке способа ответа на этот вопрос посвящено данное исследование.

Ниже после краткого воспроизведения основных моментов выполненного в [13] доказательства неустойчивости одномерных стационарных течений с ДВ_CJ развит численный метод анализа устойчивости таких течений с горением в пересжатых ДВ и приведены полученные с его помощью результаты.

1. ФОРМУЛЫ И УРАВНЕНИЯ ОДНОМЕРНОГО ПРИБЛИЖЕНИЯ ДЛЯ ТЕЧЕНИЯ С ДЕТОНАЦИОННОЙ ВОЛНОЙ В КАНАЛЕ ПЕРЕМЕННОЙ ПЛОЩАДИ

Пусть идеальный газ течет слева направо по каналу переменной площади F = F(x), где х – расстояние, отсчитываемое от стационарного положения ДВ. Если t – время; ρ, p, e, h = e + p/ρ, a и u – плотность, давление, удельные внутренняя энергия и энтальпия газа, скорости звука и газа; горючая смесь до ДВ и продукты сгорания за ней – совершенные газы с разными до и за ДВ показателями адиабаты γ₂ ≠ γ₁ и аддитивными постоянными q₁ ≠ 0 и q₂ = 0 в формулах для внутренней энергии; индекс 1 (2) метит параметры до (за) ДВ; F  ' = dF(x)/dx, D – скорость ДВ, то в одномерном приближении изучаемые нестационарные течения описываются уравнениями

уравнениями состояния и условиями на ДВ

В стационарном течении ДВ покоится (D = 0), а обыкновенные дифференциальные уравнения, получающиеся из системы (1.1), интегрируются и дают конечные равенства (последнее – следствие второго)

Здесь индекс 0 метит параметры невозмущенного (на входе в канал) потока, текущего слева направо, расход G, полная энтальпия H и удельная энтропия s – константы, G и H на ДВ не изменяются в отличие от роста энтропии и “энтропийной функции” p/ρ^γ. Независимо от этого в силу интегралов (1.3) произведение ρu (“плотность тока”) – функция числа Маха М = u/a с максимумом при М = 1. Поэтому согласно первому равенству (1.3) стационарная ДВ_CJ, за которой М₂ = 1, не может располагаться в сужающемся канале.

Для дальнейшего уравнения (1.1) запишем в характеристической форме

Первое и второе из этих уравнений определяют изменение инвариантов Римана (для изэнтропических течений) из-за переменности площади канала вдоль С⁺- и С^–-характеристик, а третье – следствие сохранения энтропии на траекториях частиц (С⁰-характеристиках).

Реализованное в разд. 3 и 4 статьи численное решение начально-краевой задачи, описывающей развитие исследуемых течений, сведено к численному интегрированию на подвижных разностных сетках законов сохранения

следствия которых – дифференциальные уравнения (1.1) и соотношения на ДВ (1.2). В (1.5) V_± = = dx_±(t)/dt – скорости правой и левой границ рассматриваемого отрезка x_–(t) ≤ x ≤ x₊(t).

На ДВ_CJ выполняются соотношения (с_р – удельная теплоемкость при постоянном давлении) [6], [13]

Здесь число Маха ДВ_CJ М_J – отношение к а₁ модуля скорости ДВ относительно газа перед ней, а D – ее скорость относительно неподвижных координат хyz.

2. НЕУСТОЙЧИВОСТЬ СТАЦИОНАРНОГО ТЕЧЕНИЯ С ДЕТОНАЦИОННОЙ ВОЛНОЙ ЧЕПМЕНА–ЖУГЕ

При числе Маха полета М₀ > M_J поток в сужающемся-расширяющемся воздухозаборнике, оставаясь сверхзвуковым, сначала тормозится до M_m < М_J в минимальном сечении, а затем разгоняется. При этом число Маха М₁ перед ДВ растет, а вместе с ним согласно последней формуле (1.3) растет величина 1/ψ. Поэтому в силу (1.6) М_J также растет, но, как показано ниже, медленнее, чем М₁ и в некотором сечении расширяющегося канала выполнится равенство М_J = М₁. В это сечение можно поставить ДВ_CJ.

Сначала, как и в [13], исследуем устойчивость стационарного течения с ДВ_CJ, приняв, что при смещении от стационарного положения ДВ_CJ остается самоподдерживающейся. Тогда при всегда справедливой последней формуле (1.3) справедлива и первая формула (1.6) и их следствие $M_{J}^{2} = M_{J}^{2}(M_{1}^{2})$. Если X_DW(t) – координата ДВ, то, учтя, что $M_{J}^{2} = M_{1}^{2}$ при X_DW = 0, получим

При сверхзвуковом течении в расширяющемся канале число Маха – растущая функция х, и знак λ определяется знаком разности в скобке, т.е. величиной стоящей в ней производной. Проделав необходимые выкладки, найдем Второе выражение получено при γ₂ = γ₁ = γ.

Согласно (2.1) при одинаковых показателях адиабаты искомая производная меньше единицы, λ > 0 и стационарное течение с ДВ_CJ неустойчиво. При разных показателях адиабаты исследование усложняется, однако и в этом случае анализ выражения в квадратных скобках в (2.1) показывает, что при реальных значениях входящих в нее параметров ситуация не изменяется: $0 < dM_{J}^{2}{\text{/}}dM_{1}^{2} < 1$ и, как отмечалось выше, M_J изменяется медленнее, чем М₁.

Если сместившаяся от своего стационарного положения ДВ_CJ станет пересжатой, то при невозмущенном набегающем потоке ее скорость станет больше скорости ДВ_CJ. При смещении ДВ вправо это может изменить вывод о неустойчивости. При смещении же ее влево большая скорость пересжатой ДВ подтвердит правильность такого вывода, чего вполне достаточно. Правда, тут же возникает вопрос о возмущениях, приходящих на ДВ справа и важных в похожих задачах с ударной волной [14]–[20]. В связи этим в [13] анализ устойчивости был проведен еще и в близкой к [14]–[20] постановке.

Итак, пусть возмущенная ДВ_CJ стала пересжатой с числом Маха М₂ < 1. Для варианта со сверхзвуковым потоком за стационарной ДВ_CJ возможную эволюцию такого течения поясняет xt-диаграмма фиг. 1. На ней начальные возмущения приходят на ДВ только слева, и при t = 0 поток возмущен лишь на малом отрезке i0 оси х так, что ДВ, став пересжатой, начала двигаться влево. При t = t_a отрезок ia С^–-характеристики придет на ДВ, и течение возмущено на отрезке ab, ограниченном справа С⁺-характеристикой, вышедшей из точки x = t = 0. Она же ограничивает возмущенное течение справа. Левая граница возмущенного течения – ДВ.

При t > 0 к пересжатой ДВ станет примыкать вначале небольшая дозвуковая область, ограниченная справа траекторией “звуковой линии” (ЗЛ), на которой u = a. Правее ЗЛ идущие против потока С^–-характеристики сносятся вправо. На ЗЛ они останавливаются, а после ее пересечения начинают движение влево вдогонку ДВ. Из сказанного и из фиг. 1 видно, что С^–-характеристики возмущенного течения – сильно искривленные кривые. Хотя все характеристики невозмущенных стационарных потоков до и за ДВ_CJ также сильно искривлены, их форма определена стационарным решением и известна заранее. В задачах, рассмотренных в [14]–[22], характеристики возмущенных и невозмущенных течений в линейном приближении совпадают, т.е. также известны.

В задаче с xt-диаграммой фиг. 1 ситуация много сложнее: теперь возмущенное течение не близко ни к какому известному. Исключение – параметры около ДВ, близкие к параметрам за ДВ_CJ. Пометив их “звездочкой” и взяв за масштабы скорости, плотности и давления ${{a}_{*}}$, ${{\rho }_{*}}$ и ${{\rho }_{*}}a_{*}^{2}$, будем иметь

с (|δu|, |δa|, |δρ|, |δp|) ≪ 1. В дополнение за масштабы площади, длины и времени возьмем F(0), l = = 1/f(0) и $l{\text{/}}{{a}_{*}}$ с f из (1.4). Если затем ввести инварианты Римана (правый δR и левый δL) и энтропийный (δS) формулами то после подстановки представлений (2.2) в уравнения (1.4) и их линеаризации характеристические уравнения в таком (“околозвуковом”) приближении примут вид В околозвуковом приближении нестационарные возмущения параметров потока выражаются через введенные инварианты равенствами

Для параметров за ДВ, пока ее отход от стационарного положения, т.е. ее координата еще мала: |X_DW(t)| ≪ 1, справедливы представления (2.2) и равенства (2.3). При этом для t > t_a сверхзвуковой стационарный поток перед ДВ невозмущен. Поэтому отличие δφ₁ любого параметра φ от его стационарного значения дается формулой: $\delta {{\varphi }_{1}}(t) = \varphi _{1}^{'}(0){{X}_{{DW}}}(t)$, в которой “штрих” означает дифференцирование по х параметра стационарного течения. Если, учтя сказанное и то, что на стационарной ДВ_CJ (при нулевой ее скорости D = 0) условия (1.2) выполняются, провести их линеаризацию, то в получившихся уравнениях не будет первой степени δL₂. Сохранив же (δL₂)², придем к равенствам (δD = dX_DW/dt – скорость ДВ)

При t = t_a неравенства в формулах (2.4) – следствие того, что, во-первых, в этот момент X_DW < 0 в силу выбора начальных возмущений, во-вторых, всегда ρ₁ < ρ₂ = 1 и u₁ > u₂ = 1, и, в-третьих, u₁ < < (γ₂ + 1)/(γ₂ – 1) в силу соотношений на ДВ и выбранных масштабов скорости и плотности. Итак, при t = t_a имеем

Следовательно, отрицательная координата X_DW(t) движущейся влево ДВ будет продолжать уменьшаться, увеличивая модуль ее также отрицательной скорости δD. Через (δL₂)² независимо от знака δL₂(t) разгону ДВ и ее удалению от стационарного положения X_DW = 0 будут способствовать любые приходящие на нее справа отраженные акустические волны. Сказанное доказывает неустойчивость стационарного течения с ДВ_CJ, к которой в стационарном решении примыкал бы справа разгоняющийся сверхзвуковой поток. Уравнения (2.4) и (2.5) и неравенства в них в согласии со способом их получения справедливы и при тормозящемся дозвуковом стационарном потоке за ДВ_CJ. Поэтому, поступая, как в предыдущем варианте, придем к выводу о неустойчивости течения и с дозвуковым потоком за стационарной ДВ_CJ.

Согласно выполненным далее расчетам, смещенная от своего стационарного положения ДВ может оставаться ДВ_CJ, а пересжатая ДВ может вновь стать ДВ_CJ (при такой эволюции течения части траектории ЗЛ и одной из С^–-характеристик даны на фиг. 1 штрихами). В этих случаях неустойчивость исследуемого течения – следствие полученного выше неравенства $dM_{J}^{2}{\text{/}}dM_{1}^{2} < 1$.

3. ЧИСЛЕННЫЙ МЕТОД РАСЧЕТА НЕСТАЦИОНАРНОЙ ЭВОЛЮЦИИ И АНАЛИЗА УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ ОДНОМЕРНЫХ ТЕЧЕНИЙ С ПЕРЕСЖАТОЙ ДЕТОНАЦИОННОЙ ВОЛНОЙ

Стационарные течения, устойчивость которых будет исследоваться далее, проще строить, решая обратную задачу с заданными γ₁, γ₂, q° = q₁/(c_p1T₀), ψ > 1 и $M_{2}^{2}$ < 1, а $M_{1}^{2}$, определяемым уравнениями (1.2) с D = 0. В такой постановке для $M_{1}^{2}$ получаются квадратное уравнение и его корень:

По заданному ψ и найденному $M_{1}^{2}$ последняя формула (1.3) определяет $M_{0}^{2}$. Задание М₂ определяет и отношение площади минимального сечения сопла F_m к площади сечения F = F_DW стационарного положения ДВ

Изучаемые ниже каналы начинаются сужающимися-расширяющимися воздухозаборниками со сверхзвуковыми числами Маха на входе (M₀), в минимальном сечении (M_m < M₀) и перед пересжатой ДВ (M₁ > M_m). Стационарная ДВ стоит в некотором сечении расширяющегося участка, плавно переходящего в цилиндрический и в сопло Лаваля. Контуры сопел либо гладкие с нулевым наклоном в минимальном сечении, либо негладкие (с внезапным сужением и положительным начальным наклоном расширяющегося участка). В гладких соплах равенство M_m = 1 в минимальном сечении x = X_m нарушают любые нестационарные возмущения, а в негладких – только достаточно интенсивные. Напомним, что при одинаковых полных длинах и расходах газа гладкие сопла заметно уступают по тяге соплам с внезапным сужением [8], [23]–[25].

Для негладких сопел сечение внезапного сужения x = X_m рассматривается в одномерном приближении как “стационарный разрыв” с выполнением законов сохранения (1.3), включая сохранение энтропии, и фиксированным отношением  f < 1 площади минимального сечения к площади цилиндрического канала. Для сохраняющихся (при небольших возмущениях потока) сверхкритического перепада давления p_m–/p₀ и М_m = 1 в минимальном сечении число Маха М_m– потока в цилиндрическом канале перед внезапным сужением – функция f и γ₂. Получающиеся в результате уравнения, определяющие сначала λ_m– (отношение скорости газа к критической скорости), а затем М_m–, имеют вид

В интервале 0 < λ_m– < 1 решение первого уравнения (3.1) единственно. Определенное по нему число Маха М_m–(f, γ₂) < 1.

Два типичных различающихся только соплами плоских канала и распределения на оси х давления с наложенным на него начальным возмущением Δр = –0.2р и числа Маха представлены на фиг. 2 для γ₁ = 1.4, γ₂ = 1.2, ψ = 2, q° = 4, М₂ = 0.8, М₁ = 2.18, М₀ = 3.81. Косые скачки рассчитывались в изэнтропическом приближении (см. [26]), что в данном случае непринципиально.

Анализ устойчивости построенных стационарных течений развивает подходы, примененные в [14]–[20] для течений с замыкающим скачком уплотнения. Отличие – в инструменте исследования – численном решении начально-краевой задачи, определяющей развитие начальных возмущений на участке канала между подвижной левой границей (ДВ) и неподвижной правой – сечением умеренно сверхзвукового потока для гладких сопел и х = Х_m для сопел с внезапным сужением.

Ранее численный расчет как инструмент изучения устойчивости течений с пересжатой ДВ, стабилизированной в расширяющемся канале, применялся в одномерном приближении с ДВ – поверхностью разрыва в [27]. В [28] при близкой к плоской ДВ рассчитались двумерные течения с детальной кинетикой горения водородно-воздушной смеси и размазанной ДВ. В [27], [28] расчеты велись по разностной схеме Годунова первого порядка аппроксимации [29]. Как и предшественники, авторы данной работы также воспользовались схемой Годунова, но повышенного на гладких решениях порядка аппроксимации [30]–[32]. Явное выделение ДВ – единственного в решаемых задачах сильного разрыва – позволяет рассчитывать на заметный эффект повышения порядка разностной схемы.

Расчет ведется на равномерной на каждом временном слое разностной сетке из N = 2^k ячеек. Границы ячеек нумеруются числами n = 0, …, N так, что n = 0 совпадает с ДВ, а n = N – с неподвижной правой границей. Значения ρ, u, e с верхним индексом n + 1/2 (по терминологии [29]: “малые параметры”) в средних точках ячеек слоев t = t_n + ντ с ν = 1/2 для “полуслоя” и с ν = 1 для нового слоя через ρ, u, e с нижним индексом n + 1/2 известного слоя t = t_n определяют следствия законов сохранения (1.5) – уравнения

Здесь Δ_n и Δⁿ = Δ_n – ντD/N – независящие от n размеры ячеек по x слоя t = t_n и полуслоя или нового слоя (D – скорость ДВ); F_n + 1/2, F ^n + 1/2, F_n, … – значения F в средних и граничных точках ячеек; R, U, P, E – значения ρ, u, p, e на границе ячейки, движущейся со скоростью V_n = (N – n)D/N, – “большие величины”, определяемые, как и скорость ДВ D, из решения задачи о распаде разрыва.

Как в [31], уравнения (3.2) сначала определяют малые величины в ячейках полуслоя. Этому предшествует нахождение предраспадных параметров на границах ячеек слоя t = t_n (экстраполяцией для n = 0 и N и интерполяцией согласно [30] для 1 ≤ n ≤ N – 1). По ним расчетом распада разрыва находятся большие величины в правых частях уравнений (3.2) и в каждой ячейке последовательно определяются ρ ^n + 1/2, u ^n + 1/2, e ^n + 1/2 и p ^n + 1/2 = (γ₂ – 1)(ρe)^n + 1/2. Отличие проводимого затем счета нового слоя состоит в том, что большие величины, площади F_n и F_n + 1 и скорость ДВ D, а по ней скорости границ V_n и V_n + 1 находятся на полуслое.

Явно выделяемая ДВ может оставаться пересжатой, а может стать ДВ_CJ. Этим возможностям отвечают разные задачи о распаде, начиная с предраспадных параметров и xt-диаграмм. При распаде с пересжатой ДВ (фиг. 3а) левые (с индексом I вместо 1) предраспадные “малые” параметры при x₀ = X_DW0 берутся из стационарного решения, а правые также “малые” (с индексом II) линейно экстраполируются на x = X_DW0 по двум ячейкам слоя t = t_n или t = t^{n + 1/2}. Как в [29, § 13], для пересжатой ДВ из законов сохранения (1.2) получаются соотношения

в которых P и U – давление и скорость, непрерывные на слабом контактном разрыве (КР), а R_I и A_I суть ρ и а слева от КР. При изучении устойчивости на всегда слабой “правой” волне (ПВ, неважно, ударной или волне разрежения) с погрешностью порядка (1 – p_II/P)³ верны равенства (R_II и A_II суть ρ и а справа от КР) Подстановка $A_{{II}}^{2}$ во второе из этих уравнений дает квадратное уравнение для R_II, решив которое и взяв положительный корень, получим Разрешив относительно P первые уравнения (3.3) и (3.5), придем к формуле

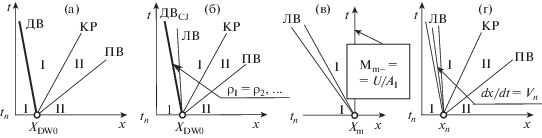
Уравнение (3.7) с j из (3.4) и B_II из (3.6) решается итерациями с P⁽⁰⁾ = p_II. По завершении итераций формулы (3.3) дают U, R_I, A_I и скорость ДВ D. Координата ДВ X_DW находится интегрированием с шагом ντ уравнения dX_DW/dt = D от t = t_n и X_DW = X_DW0 cо скоростью D, найденной для полуслоя при t = t_n, а для нового слоя – на полуслое. Прежде чем сделать новый временной шаг, по последней формуле (3.3), вычисляется число Маха М₂ и новый шаг делается, если найденное M₂ ≤ 1. В противном случае реализуется переход к ДВ_CJ (фиг. 3б). При неизменных p₁, … параметры за ДВ_CJ (с индексом I вместо 2) находятся по формулам (1.6), а для примыкающей к ней слабой (согласно расчетам – на достаточно мелких сетках) “левой” волны разрежения (ЛВ) верны столь же точные, как равенства (3.5), соотношения

Отсюда аналогично уравнению (3.6) для R^II получается уравнение а для по-прежнему слабой “правой волны” верны равенства (3.5). Разрешив первые уравнения (3.5) и (3.8) относительно P, придем к формуле С привлечением уравнений (3.6) и (3.9) для R_II и R_I и формул для A_I и A_II итерациями находятся P, R_I, R_II, A_I и A_II, а затем U. Из них далее нужно только Р, но не для вычисления правых частей уравнений (3.2) с n = 0 и координаты ДВ X_DW. Для этого хватает параметров с индексом 2 (замененным на I), определенных формулами (1.6) до решения задачи о распаде разрыва. Давление Р определяет, сохраняется ли ДВ_CJ или следует вернуться к пересжатой ДВ: первое – при Р ≤ р_I = р₂, второе – при P > р_I = р₂.

Для канала с гладким соплом в качестве неподвижной правой границы берется сечение на таком удалении от минимального сечения сопла, что возмущенный поток в нем при t > 0 сверхзвуковой. Большие величины в этом сечении находятся экстраполяцией по известным параметрам при t = t_n или t = t ^n + 1/2. Для каналов с внезапным сужением правая граница – сечение x = X_m. Предраспадные u_I, p_I и ρ_I также экстраполируются в сечение x = X_m по параметрам слоя t = t_n или полуслоя. При t > 0 в этом сечении известен определенный формулами (3.1) квадрат числа Маха M_m–, причем $M_{{m - }}^{2} = {{U}^{2}}{\text{/}}A_{I}^{2} = {{U}^{2}}{{R}_{I}}{\text{/}}({{\gamma }_{2}}P)$. В слабой левой волне (ЛВ на фиг. 3в) выполняются равенства (3.8). Подстановка U и R_I из (3.8) в уравнение $M_{{m - }}^{2} = {{U}^{2}}{{R}_{I}}{\text{/}}({{\gamma }_{2}}P)$ дает кубическое уравнение для P и его следствие

Правильное (близкое к р_I,) значение P находится итерациями с привлечением решения (3.9) для R_I.

Описанный нелинейный подход справедлив и при определении больших величин на внутренних границах (фиг. 3г, 1 ≤ n ≤ N – 1). Для них итерациями решается уравнение (3.10) с решениями (3.6) и (3.9) для R_II и R_I. По завершении итераций одинаковые значения U дают формулы из (3.5) и (3.8).

Если ЛВ – слабая ударная волна, то ее скорость [8]: D_I = (u_I – a_I + U – A_I)/2 и большие величины для уравнений (3.2) выбираются так:

Если же ЛВ – волна разрежения, то возможны три варианта: Третий вариант реализуется при u_I – a_I < V < U – A_I (фиг. 3г, граница внутри ЛВ разрежения). Здесь найденные из распада разрыва большие величины заменяются на A, …, последовательно вычисляемые по приведенным формулам.

Как показали расчеты, описанная разностная схема, использующая идеи схем [30]–[32 ], устойчива при τ ≤ Δ/(u + a – V)_max с максимумом по ячейкам слоя t = t_n.

4. ПРИМЕРЫ РАСЧЕТА

Приводимые далее примеры рассчитаны по программе, составленной в рамках описанных выше математической модели и разностной схемы для двигателеподобных каналов типа изображенных на фиг. 2а. В выполненных расчетах задавались постоянные одинаковые относительные начальные возмущения δφ = Δφ/φ скорости, плотности и давления на отрезке, показанном на фиг. 2б. Заданные так начальные возмущения порождают три волны: две акустические, бегущие влево (“L-волна”) и вправо (“R-волна”), и сносимую потоком энтропийную – “S-волну”. На ДВ первой приходит начальная L-волна, а затем L-волны – отражения R- и S-волн от сужения сопла. При |δφ| < ε, где ε – достаточно малая величина, для таких начальных возмущений исследуемые течения возвращались к своим стационарным состояниям. Как и следовало ожидать, величина ε убывает с приближением М₂ к единице и при одинаковых степенях поджатия f с переходом от гладкого сопла к соплу с внезапным сужением. Неочевидным оказалось уменьшение ε при переходе от отрицательных δφ к положительным и рост ε с увеличением q° при фиксированных остальных параметрах обратной задачи, определяющих стационарное течение.

Иллюстрации сказанного предпошлем фиг. 4, показывающую зависимость результатов расчета от количества ячеек N = 2^k для канала фиг. 2 с внезапным сужением при δφ = 0.16. Несмотря на отнюдь не малое возмущение, расчеты на сетках с k = 7–11 до t = 20 (время отнесено к y₀/u₀ с размерными высотой входа в канал y₀ и скоростью u₀) продемонстрировали возврат к стационарному течению при двукратном переходе пересжатой ДВ к ДВ_CJ и обратно. Два фрагмента верхней фигуры с растянутыми осями демонстрируют линейную сходимость на грубых сетках (k = 7 и 8), переходящую в квадратичную с измельчением сетки. В исходных масштабах кривые для k = 10 и 11 неразличимы.

Непосредственное сравнение результатов, полученных при расчете с применением развитой разностной схемы и схемы первого порядка аппроксимации на непрерывных решениях для одного из фрагментов фиг. 4, представлено на фиг. 5. Схема первого порядка получается из описанной разностной схемы исключением счета полуслоя и использованием в качестве предраспадных параметров малых величин с полуцелыми нижними индексами. Поэтому счет по ней идет в два раза быстрее. Однако, согласно фиг. 5, результаты одинакового качества получаются по этой схеме при увеличении числа ячеек в 2² раза и уменьшении шага интегрирования τ в те же 2² раза. В итоге – рост времени счета в 2³ раз, а при решении двумерных и пространственных задач в 2⁵ и в 2⁷ раз.

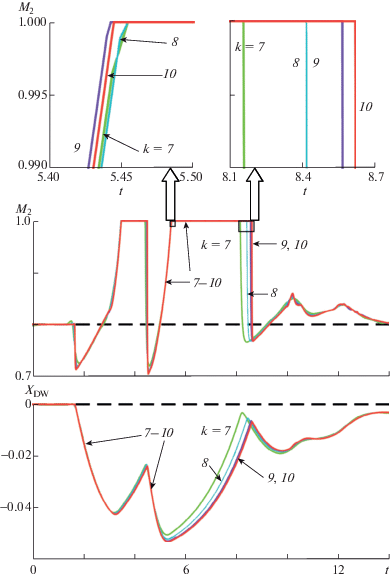
Переход к ДВ_CJ происходит под воздействием пришедших сзади на пересжатую ДВ L-волн разрежения. При этом, как показали расчеты, формируется примыкающая к ДВ_CJ интенсивная волна разрежения. Для правильного описания этого процесса расчетная сетка в окрестности ДВ_CJ должна быть достаточно мелкой.

Три примера расчета на сетках с k = 10 (N = 1024) для двух каналов фиг. 2 и стационарных течений в них демонстрирует фиг. 6. На ней для |δφ| = 0.2 приведены зависимости от t числа Маха М₂ и координаты ДВ X_DW. При δφ = 0.2 для сопла с внезапным сужением второй переход к ДВ_CJ закончился разрушением стационарного течения. Для гладкого сопла этого не происходит из-за меньшего отражения приходящих к нему акустических и энтропийных волн. Согласно фиг. 4 при δφ ≤ 0.16 возмущения затухают и для канала с внезапным сужением. Затухают возмущения и при больших отрицательных возмущениях (фиг. 6, δφ = – 0.2).

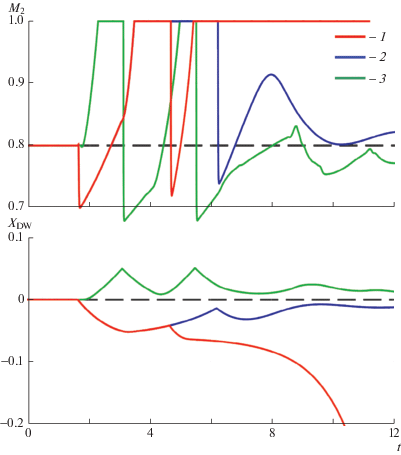
В четырех случаях, показанных на фиг. 4 и 6, реализуется двукратный или однократный переход к ДВ_CJ. В трех из них при равном числе обратных переходов восстанавливалось исходное стационарное течение с пересжатой ДВ, причем на фиг. 4 и в случае 2 на фиг. 6 – после смещения ДВ против потока. Обратный переход осуществляют волны сжатия, интенсивность которых достаточна для ликвидации волн разрежения, сопровождающих ДВ_CJ. В случае 1 на фиг. 6 обратного перехода не произошло и ДВ, сместившись против потока, став ДВ_CJ и оставаясь таковой (в реальности до попадания в плохо перемешанную горючую смесь), продолжает движение в том же направлении.

ЗАКЛЮЧЕНИЕ

Отличие развитого подхода от также “численных” подходов предшественников [27], [28] в счете по более аккуратной разностной схеме, в упрощениях, обусловленных слабостью всех, кроме ДВ, волн в задачах о распаде разрыва, в нацеленности на двигателеподобные конфигурации (в частности, с внезапно сужающейся дозвуковой частью сопла Лаваля) и в интересных примерах с переходами к ДВ_CJ и обратно. Вместе с оправданным для рассматриваемых задач использованием простых (“классических”) моделей термодинамики и газовой динамики одномерных течений с ДВ – поверхностью разрыва это позволило создать достаточно аккуратный, быстрый и адекватный инструмент решения задач, интересных для теории и приложений.

Для устойчивых к малым возмущениям стационарных течений с пересжатой ДВ в канале с сильно отражающим нестационарные возмущения внезапным сужением сравнительно большие возмущения приводят к переходу пересжатой ДВ на режим ДВ_CJ. При сдвиге ДВ по потоку в таких случаях наблюдаются обратный переход и возврат к исходному стационарному течению. Обратного перехода может не произойти, если возникшие из-за больших возмущений ДВ_CJ и примыкающая к ней достаточно интенсивная волна разрежения сдвинулись против потока. В таких случаях движение ДВ_CJ в том же направлении будет продолжаться до ее попадания в плохо перемешанную горючую смесь.

Авторы благодарны А.Н. Кудрявцеву за полезные замечания.