Химия высоких энергий, 2020, T. 54, № 6, стр. 423-432
Фотоэффект в органических солнечных элементах на основе фталоцианинов. I. Термическая ионизация молекулярных экситонов
В. А. Бендерский a, *, И. П. Ким a
a Институт проблем химической физики РАН
142432 Московская обл., Черноголовка, просп. Академика Семенова, 1, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 06.04.2020
После доработки 06.04.2020
Принята к публикации 20.04.2020
Аннотация
На основании полученных ранее данных [1, 2], согласно которым квантовый выход фотоэффекта (Y) в кристаллах b – формы фталоцианинов без металла(I) и меди(II) одинаков для электронов и дырок и обладает аррениусовской зависимостью от температуры с энергией активации ${{E}_{Y}},$ равной разности ширины запрещенной зоны и энергии молекулярных экситонов (МЭ), предложена трехмерная стохастическая модель термической ионизации МЭ, рассматриваемой как последовательность обратимых переходов из МЭ в низшее состояния с переносом заряда (СПЗ) и затем в СПЗ с растущей длиной переноса. Найдено соотношение между ${{E}_{Y}}$ и радиальной плотностью СПЗ, при которой вероятность разделения зарядов больше, чем гибели СПЗ.
I. ВВЕДЕНИЕ
Многолетние исследования фотоэффекта в органических материалах недавно ознаменовались созданием лабораторных образцов органических солнечных элементов (ОСЭ) с высоким (до 17%) коэффициентом преобразования солнечного излучения в электрическую энергию [3–14]. Основное отличие ОСЭ от устройств на основе неорганических полупроводников состоит в том, что поглощение света обусловлено внутримолекулярными оптическими переходами, при которых образуются не носители тока, а молекулярные экситоны (МЭ), способные переносить энергию, но не создающие фототок.
Прогресс в создании эффективных ОСЭ достигнут для большого числа веществ с различным составом и строением молекул, обладающих, тем не менее, рядом общих свойств, определяющих их эффективность в составе ОСЭ. Установить эти свойства и определить их количественные характеристики – очевидная, но еще не решенная задача. Один из возможных путей ее решения – выбрать одно из достаточно хорошо изученных веществ, применяемых в ОСЭ, и на его примере проследить предполагаемые механизмы образования и переноса МЭ и носителей тока. Одними из таких веществ являются фталоцианины (Рс) различных металлов – искусственные красители, близкие по строению к порфирину, основному компоненту собирающих свет природных агрегатов [15]. Рс обладают высокой термической устойчивостью (в молекуле отсутствуют химические связи с энергиями разрыва, меньшими 70 Ккал/моль), легко очищаются до содержания примесей ~ 1 ppm и доступны как в виде кристаллов, так и микронных и субмикронных слоев, применяемых ОСЭ. Перечислим основные свойства фталоцианинов, оправдывающие их выбор в качестве эталона: 1) кристаллографическая упаковка плоских молекул в стопки с параллельным расположением их плоскостей на расстоянии Ван-дер-Ваальсова контакта (~0.4 нм), и расстоянием между стопками, определяемым размерами молекулы в плоскости (~1.3 нм); 2) интенсивные полосы экситонного поглощения с 00-переходом в области энергии МЭ (${{E}_{S}}$ = 1.71–1.74 эВ для фталоцианина без металла Н2Рс); 3) ширина запрещенной зоны $\Delta $ = 1.94–1.97 эВ и отсутствие межзонных переходов [16, 17]; 4) узкие (шириной, меньше 0.1 эВ) зоны разрешенной энергии как МЭ, так и носителей тока; 5) образование состояний с переносом заряда и смешанных кристаллов с молекулами акцепторов, обладающими более высоким сродством к электрону, чем молекулы Рс. Все перечисленные характеристики присущи большинству материалов для ОСЭ [18].
В этой серии статей мы представим сравнительный обзор основных оптических и фотоэлектрических свойств кристаллов и поликристаллических слоев Рс вместе с теоретическим описанием этих свойств в моделях, большинство из которых появилось намного позднее результатов измерений. Ранее систематическое сопоставление экспериментальных данных с этими теоретическими представлениями не проводилось.
В первом разделе статьи рассмотрена термическая ионизация МЭ, обусловленная тем, что разность $\Delta - {{E}_{S}}$ лишь в ~10 раз превышает тепловую энергию (в Н2Рс ${{(\Delta - {{E}_{S}})} \mathord{\left/ {\vphantom {{(\Delta - {{E}_{S}})} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}$ = 8–10 при 300 К), что позволяет детектировать образование и перенос носителей тока, пользуясь результатами импульсных фотоэлектрических измерений, обладающих высокой чувствительностью и позволяющих детектировать малые изменения заряда (>10–9 Кл). Процесс ионизации рассматривается как последовательность обратимых переходов между состояниями с переносом заряда (СПЗ), которым принадлежит ключевая роль в фотоэффекте в органических материалах. Кинетическая модель таких переходов позволяет представить квантовый выход фотоэффекта в виде отношения вероятностей прямых и обратных переходов между СПЗ и выявить условия, при которых МЭ и СПЗ превращаются в носители тока быстрее, чем гибнут. Экспериментальные данные собраны во втором разделе. Трехмерная кинетическая модель превращения МЭ в носители тока с промежуточным обратимым образованием СПЗ с растущей длиной переноса заряда рассмотрена в третьем разделе, где показано, что отношение скоростей прямых и обратных переходов зависит от разности энергий и радиальной плотности СПЗ, которая в четвертом разделе представлена в виде огрубленного разложения по стохастическим шаровым слоям, образующимся в результате перемешивания состояний с близкой длиной переноса в процессе ее роста. В пятом и шестом разделах найдены квантовый выход фотоэффекта и распределение концентраций СПЗ.
II. КВАНТОВЫЙ ВЫХОД ФОТОЭФФЕКТА
В спектре отражения света, поляризованного по кристаллографическим осям $a$ и $b$($a \bot b$), в кристаллах H2Pc и CuPc при 4.2 и 77 К наблюдаются длинноволновые полосы с максимумами 1.71(1.77) и 1.71(1.74) эВ соответственно. Полуширина полос ~400 см–1, давыдовское расщепление 320–350 см–1, поляризационное отношение 3.0–3.6. Высокая поляризация и наличие расщепления показывают, что в результате оптического перехода образуются МЭ, отличающиеся от локализованных возбужденных состояний молекул тем, что их время жизни больше, чем перехода между соседними узлами. Ширина полос свидетельствует о сильном электронно-колебательном взаимодействии, типичном для молекулярных кристаллов, например, кристаллов антрацена, тетрацена и пентацена [19].
Квантовый выход фотоэффекта измерен методом кристаллического счетчика под действием импульсов света с длиной волны 580, 625, и 670 нм длительностью 20 нс [1]. Число фотонов измерялось независимо, так что отношение образующегося числа электронов к числу фотонов позволяло найти абсолютные значения квантового выхода. Квантовый выход электронов и дырок определяется величиной заряда в условиях насыщения, когда на коллекторе собираются все образовавшиеся носители тока. Поглощение света в слое ${{\sim {\kern 1pt} 1} \mathord{\left/ {\vphantom {{\sim {\kern 1pt} 1} k}} \right. \kern-0em} k}$ ≈ ≈ 0.3 мкм создает зону генерации носителей тока с квазистационарной концентрацией МЭ (длительность импульса накачки много больше ${{\tau }_{S}}$ ≈ ≈ (2–4) × 10–11с [20, 21]), из которой внешнее электрическое поле ${{V}_{0}}$ = 102–103 В полностью извлекает образующиеся носители тока с подвижностью $\mu $ (${{\mu }_{n}}$ ≈ ${{\mu }_{p}}$ ≈ 0.5 см2/Вс, время пролета зоны $\sim {\kern 1pt} {{({{k}^{2}}\mu {{V}_{0}})}^{{ - 1}}}$ больше времени жизни МЭ и короче времени рекомбинации в ней носителей тока). Измерения выполнены при направлении освещения и приложенного электрического поля вдоль нормали к плоскости кристалла $ab.$ Проводимость кристаллов H2Pc и CuPc близка к собственной ((1–2) × 10–15 и (7–8) × 10–15 ом–1 см–1 соответственно) в интервале температур 250–350 К.
Результаты сводятся к следующим. Квантовый выход фотоэффекта электронов и дырок одинаков во всем температурном интервале, не зависит от длины волны света и описывается аррениусовской зависимостью
(1)
$Y = {{Y}_{n}} = {{Y}_{p}} = {{Y}_{0}}\exp ({{ - {{E}_{Y}}} \mathord{\left/ {\vphantom {{ - {{E}_{Y}}} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}).$При 290 К значения квантового выхода равны (3–7) × 10–5 и (1–3) × 10–5, энергии активации –0.19 и 0.25 эВ для кристаллов H2Pc и CuPc соответственно.
Зависимость (1) выполняется, если фотоэффект обусловлен либо межзонным переходом с участием колебательно возбужденных молекул в основном электронном состоянии, либо термической ионизацией образующихся МЭ. В первом механизме зависимость (1) должна исчезать, когда энергия фотонов $\hbar \Omega $ становится больше ширины запрещенной зоны $\Delta ,$ что не наблюдалось. Подобная зависимость $Y(\Omega )$ имела бы место и при ионизации колебательно возбужденных МЭ с энергией, большей $\Delta .$ Отсутствие зависимости квантового выхода от энергии фотонов говорит также о том, что поглощение света сопровождается быстрой колебательной релаксацией МЭ, которая предшествует последующей ионизации МЭ в основном колебательном состоянии. Из условия ионизационного равновесия скорость ионизации равна
(2)
${{W}_{S}} = {{\gamma }_{{np}}}\frac{{{{N}_{c}}{{N}_{{v}}}}}{{{{N}_{s}}}}\exp ({{ - (\Delta - {{E}_{S}})} \mathord{\left/ {\vphantom {{ - (\Delta - {{E}_{S}})} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}),$(3)
$Y = {{\left( {{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} {{{W}_{S}}{{\tau }_{S}}}}} \right. \kern-0em} {{{W}_{S}}{{\tau }_{S}}}}} \right)}^{{ - 1}}}.$Поскольку для узких зон плотности состояний одного порядка с плотностью молекул (в кристаллах Рс ${{N}_{0}}$ = 2 × 1021 см–3) и $Y \ll 1,$ из (1)–(3) следует, что скорости бимолекулярной рекомбинации и гибели МЭ одного порядка
(4)
${{\gamma }_{{np}}}{{N}_{0}} \approx {1 \mathord{\left/ {\vphantom {1 {{{\tau }_{S}}}}} \right. \kern-0em} {{{\tau }_{S}}}}.$При указанном выше значении ${{\tau }_{S}}\,\,{{\gamma }_{{np}}}$ = 10–10–10–9 см3 с–1, что более чем на два порядка меньше ожидаемой константы скорости кулоновского захвата (~10–7 см3 с–1) частицы с массой свободного электрона ${{m}_{0}}$ и тепловой скоростью ${{({{2{{k}_{B}}T} \mathord{\left/ {\vphantom {{2{{k}_{B}}T} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Причинами различия могут быть узкие зоны носителей тока, в которых эффективная масса на порядки больше ${{m}_{0}},$ и образование промежуточных состояний с сечениями захвата большими, чем образования МЭ. Хотя МЭ является ближайшим по энергии детектируемым состоянием к электронно-дырочной паре, между ними расположена последовательность состояний с переносом заряда (СПЗ), которые являются промежуточными в процессе рекомбинации. Эти состояния характерны для 1 : 1 комплексов, состоящих из молекул донора и акцептора [22–24]. Хотя в спектрах однокомпонентных молекулярных кристаллов СПЗ не удается детектировать на фоне интенсивных полос МЭ, спектр СПЗ детально изучен теоретически на примере одномерной модели молекулярного кристалла [25–28]. Одномерная модель не только допускает точное аналитическое решение задачи на собственные значения, но и позволяет найти условия, при которых возрастает квантовый выход фотоэффекта, в частности, при увеличении матричных элементов переноса. В [29, 30] предсказано, что в одномерной модели ионизация СПЗ в сильных электрических полях, возникающих в тонких $pn$-переходах, способна обеспечить квантовый выход, близкий к 1. Однако участие СПЗ в кинетике ионизации МЭ в трехмерных кристаллах ранее не рассматривалась. Основная цель этой статьи – показать, что в трехмерной среде вероятность ионизации МЭ и СПЗ на порядки выше предсказываемых одномерной моделью.
III. ИОНИЗАЦИЯ ЭКСИТОНОВ –ПОСЛЕДОВАТЕЛЬНОСТЬ ПЕРЕХОДОВ МЕЖДУ СПЗ
В условиях теплового равновесия ионизация МЭ связана с образованием низшего СПЗ ${{C}_{1}}$ (НСПЗ), в котором электрон и дырка локализованы на соседних узлах решетки, расположенных по оси стопки $\vec {b}$ на расстоянии постоянной решетки $b,$ в котором кулоновская связь между ними максимальна, но меньше, чем в МЭ. В следующем по энергии СПЗ ${{C}_{2}}$ дырка остается на том же узле, а электрон занимает один из узлов второй координационной сферы, принадлежащих либо той же стопке на расстоянии $2b,$ либо одной из соседних стопок, на расстоянии, определяемом постоянными решетки $a,c \gg b.$ По такой же схеме образуются высшие СПЗ $n \geqslant 3,$ спектр которых сходится ко дну зоны проводимости, если локализована дырка, так что энергия СПЗ в трехмерной решетке определяется совокупностью трех целых чисел
определяющих число периодов решетки по ее осям. В противоположном случае локализации электрона, следом за НСПЗ образуются состояния, в которых дырка последовательно занимает узлы в других стопках, удаляясь от электрона. В одномерной модели смещение обоих зарядов вдоль цепочки узлов учитывается переходом к новым разделяющимся переменным – смещению центра тяжести СПЗ как целого и расстоянию между зарядами. Движение центра тяжести определяет ширину зон СПЗ, а изменение расстояния – изменение собственных значений кулоновской энергии зарядов при переходах $\Delta n$ = ±1. При экспоненциально малом перекрывании молекулярных орбиталей соседних узлов, типичном для молекулярных кристаллов, матричные элементы переноса электрона и дырки по отдельности много больше, чем их переноса вместе, так что СПЗ с $n \geqslant 2$ быстрее распадаются, чем перемещаются как целое, т.е. являются не экситонами, а локализованными возбужденными состояниями [19, 30].
Отметим различие МЭ и СПЗ. Матричные элементы экситонного переноса определяют сильное дальнодействующее диполь-дипольное взаимодействие, присущее интенсивным излучательным переходам. В противоположность МЭ, дипольные моменты вертикальных оптических переходов из основного состояния в СПЗ малы из-за малых факторов Франка–Кондона, так что матричные элементы диполь-дипольного переноса и ширина зоны СПЗ даже по оси $b$ малы, по сравнению с экситонной, и становится еще меньше по осям с большей длиной переноса. Если пренебречь матричными элементами переноса СПЗ, собственные значения их энергии определяются диагональными элементами кулоновского взаимодействия электрона и дырки, локализованных на узлах решетки 0 и $n,$ которые можно представить эмпирическим соотношением
(6)
${{U}_{n}} = {{ - {{U}_{1}}} \mathord{\left/ {\vphantom {{ - {{U}_{1}}} {R(n)}}} \right. \kern-0em} {R(n)}},$(7)
${{S}_{0}}\begin{array}{*{20}{c}} {\xrightarrow{I}} \\ {\xleftarrow{{{1 \mathord{\left/ {\vphantom {1 {{{{\tau }}_{S}}}}} \right. \kern-0em} {{{{\tau }}_{S}}}}}}} \end{array}{{S}_{1}}\begin{array}{*{20}{c}} {\xrightarrow{{{{W}_{{01}}}}}} \\ {\xleftarrow{{{{W}_{{10}}}}}} \end{array}{{C}_{1}}\begin{array}{*{20}{c}} {\xrightarrow{{{{W}_{{12}}}}}} \\ {\xleftarrow{{{{W}_{{21}}}}}} \end{array}{{C}_{2}}...{{C}_{{s - 1}}}\begin{array}{*{20}{c}} {\xrightarrow{{{{W}_{{s - 1,s}}}}}} \\ {\xleftarrow{{{{W}_{{s,s - 1}}}}}} \end{array}{{C}_{s}}...$известна как кинетический процесс Беккера–Деринга, изучаемый в теории неразветвленных цепных реакций [35]. Кинетические уравнения для концентраций МЭ и огрубленных СПЗ в схеме (7) имеют вид
(8)
$\begin{gathered} {{{\dot {S}}}_{1}} = I - \left( {\tau _{S}^{{ - 1}} - {{W}_{{01}}}} \right){{S}_{1}} + {{W}_{{10}}}{{C}_{1}}, \\ {{{\dot {C}}}_{1}} = {{W}_{{01}}}{{S}_{1}} - \left( {{{W}_{{10}}} + {{W}_{{12}}}} \right){{C}_{1}} + {{W}_{{21}}}{{C}_{2}},... \\ {{{\dot {C}}}_{s}} = {{W}_{{s - 1,s}}}{{C}_{{s - 1}}} - \left( {{{W}_{{s,s - 1}}} + {{W}_{{s,s + 1}}}} \right){{C}_{s}} + \\ + \,\,{{W}_{{s + 1,s}}}{{C}_{{s + 1}}},\,\,\,\,s \geqslant 2. \\ \end{gathered} $Первое уравнение учитывает оптическую накачку перехода ${{S}_{0}} \to {{S}_{1}},$ гибель МЭ и его превращение в НСПЗ. Второе уравнение для концентрации НСПЗ включает их образование из МЭ, гибель ${{C}_{1}} \to {{S}_{1}},$ ${{S}_{0}}$ (обратный переход в МЭ и переход в основное состояние) и превращение в ${{C}_{2}}.$ Вероятности переходов ${{W}_{{s,s{\kern 1pt} '}}}$ удовлетворяют условиям детального равновесия, постулирующим равенство скоростей прямых и обратных переходов при тепловом равновесии
(9)
$\begin{gathered} {{W}_{{s,S + 1}}}{{{\bar {C}}}_{s}} = {{W}_{{s + 1,s}}}{{{\bar {C}}}_{{s + 1}}},\,\,\,\,{{{{{\bar {C}}}_{{s + 1}}}} \mathord{\left/ {\vphantom {{{{{\bar {C}}}_{{s + 1}}}} {{{{\bar {C}}}_{s}}}}} \right. \kern-0em} {{{{\bar {C}}}_{s}}}} = \\ = \left( {{{{{N}_{{s + 1}}}} \mathord{\left/ {\vphantom {{{{N}_{{s + 1}}}} {{{N}_{s}}}}} \right. \kern-0em} {{{N}_{s}}}}} \right)\exp \left( {{{({{E}_{s}} - {{E}_{{s + 1}}})} \mathord{\left/ {\vphantom {{({{E}_{s}} - {{E}_{{s + 1}}})} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right), \\ \end{gathered} $(8) и (10) определяют совокупность концентраций, зависящих от одного параметра – квантового выхода, равного отношению сквозного тока к току оптической накачки
(11)
$\begin{gathered} Y = {J \mathord{\left/ {\vphantom {J I}} \right. \kern-0em} I} = \left( {1 + {{q}_{1}} + {{q}_{1}}{{q}_{2}} + {{q}_{1}}{{q}_{2}}{{q}_{3}} + } \right. \\ {{\left. { + \,\,.... + {{q}_{1}}{{q}_{2}}{{q}_{3}}...{{q}_{s}} + ...} \right)}^{{ - 1}}}, \\ \end{gathered} $(12)
${{q}_{s}} = {{{{W}_{{s,s - 1}}}} \mathord{\left/ {\vphantom {{{{W}_{{s,s - 1}}}} {{{W}_{{s,s + 1}}}}}} \right. \kern-0em} {{{W}_{{s,s + 1}}}}}.$Следует отметить, что в схеме Беккера–Деринга квантовый выход зависит не от абсолютных значений вероятностей переходов, а только их отношений, что упрощает кинетическую задачу в случае огрубленных распределений, удовлетворяющих условиям детального равновесия (9). Энергии активации прямых и обратных электронных переходов $s \leftrightarrow s{\kern 1pt} '$ связаны с разностью свободных энергий начального и конечного состояний факторами симметрии ${{\alpha }_{{nn{\kern 1pt} '}}}$
(13)
$\begin{gathered} G_{{nn{\kern 1pt} '}}^{\# } = {{G}_{R}} + {{\alpha }_{{nn{\kern 1pt} '}}}({{G}_{n}} - {{G}_{{n{\kern 1pt} '}}}), \\ G_{{n{\kern 1pt} 'n}}^{\# } = {{G}_{R}} + (1 - {{\alpha }_{{nn{\kern 1pt} '}}})({{G}_{{n{\kern 1pt} '}}} - {{G}_{n}}) \\ 0 \leqslant {{\alpha }_{{nn{\kern 1pt} '}}} \leqslant 1, \\ \end{gathered} $(14)
${{\alpha }_{{nn{\kern 1pt} '}}} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$Выражения (13) и (14) позволяют переписать (11)
(15)
$\begin{gathered} Y = \left( {1 + {{{\left( {{{W}_{{01}}}{{\tau }_{S}}} \right)}}^{{ - 1}}}\left( {1\, + \sum\limits_n {\exp ({{ - \left( {{{G}_{n}}\, - {{G}_{S}}} \right)} \mathord{\left/ {\vphantom {{ - \left( {{{G}_{n}}\, - {{G}_{S}}} \right)} {2{{k}_{B}}T}}} \right. \kern-0em} {2{{k}_{B}}T}}} } \right)} \right. \times \\ \times \,\,{{\left. {\exp {\kern 1pt} \left( {{{ - \left( {\Delta - {{E}_{S}}} \right)} \mathord{\left/ {\vphantom {{ - \left( {\Delta - {{E}_{S}}} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)_{{}}^{{_{{_{{}}^{{}}}}}}} \right)}^{{ - 1}}}. \\ \end{gathered} $Выражение (15) имеет тот же вид, что и феноменологическое соотношение (2), отличаясь от него префактором, в котором сумма учитывает уменьшение квантового выхода за счет обратных переходов в СПЗ. Этот префактор позволяет сделать важный вывод, не прибегая к численным расчетам. Если плотности состояний ${{N}_{n}}$ не увеличиваются с ростом $n,$ а энергия кулоновской связи монотонно уменьшается, так что при больших $n$ значения
(16)
$\begin{gathered} {{q}_{n}} = \exp \left( {{{\left( {{{G}_{{n - 1}}} - {{G}_{{n + 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{G}_{{n - 1}}} - {{G}_{{n + 1}}}} \right)} {2{{k}_{B}}T}}} \right. \kern-0em} {2{{k}_{B}}T}}} \right) = \\ = \left( {\frac{{{{N}_{{n - 1}}}}}{{{{N}_{{n + 1}}}}}} \right)\exp \left( {{{\left( {{{G}_{{n - 1}}} - {{G}_{{n + 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{G}_{{n - 1}}} - {{G}_{{n + 1}}}} \right)} {2{{k}_{B}}T}}} \right. \kern-0em} {2{{k}_{B}}T}}} \right) \geqslant 1 \\ \end{gathered} $ряд в (15) расходится и квантовый выход равен нулю. Скорости обратных переходов больше, чем прямых и концентрации ${{C}_{n}}$ экспоненциально уменьшаются. Эта ситуация соответствует одномерной цепочке, в которой плотность состояний постоянна и конечные значения $Y$ возникают только за счет внешнего электрического поля, компенсирующего кулоновское притяжение [29]. Когда длина переноса $n$ (число постоянных решетки, разделяющих узлы, на которых локализованы электрон и дырка) превышает значение $n*,$ при котором электронно-дырочный потенциал максимален, скорость обратных переходов становится меньше, чем прямых [29].
В трехмерном кристалле появляется еще одна причина разделения зарядов, обусловленная ростом плотности состояний с ростом $n.$ Поэтому расчет квантового выхода ионизации МЭ нельзя ограничить решением одномерной задачи, а необходимо предварительно найти плотность СПЗ в трехмерном кристалле.
IV. РАДИАЛЬНАЯ ПЛОТНОСТЬ СПЗ В МОНОКЛИННОЙ РЕШЕТКЕ
Плотность СПЗ, образующихся при переносе электрона от молекулы в узле (0, 0, 0) на молекулу в узле, определяемом тремя целыми числами (${{n}_{a}},$ ${{n}_{b}},$ ${{n}_{c}}$), определяется расстоянием между этими узлами
(17)
$P(R) = \sum\limits_n {\delta (R - {{R}_{n}})} ,\,\,\,{{R}_{n}} = R\left( {{{n}_{a}},{{n}_{b}},{{n}_{c}}} \right).$Результаты расчета $R(n)$ для моноклинной решетки Рс ($a$ = 1.96, $b$ = 0.47, $c$ = 1.48 нм, $\beta $ = 122°), с направлением стопок по оси $b$ с наименьшей постоянной решетки, представлен на рис. 1. При $R$ < 1 нм, ${{n}_{a}} = 0,$ ${{n}_{b}} = 1,2,$ ${{n}_{c}} = 0,$ перенос происходит только в стопке по оси $b.$ В узком интервале $3 \leqslant N$ = $\bmod (n) \leqslant 4$ в сумму входят ближайшие узлы соседних стопок, расположенные в плоскостях $(ab)$ и ($bc$), а при $N$ > 4 плотность определяют комбинации узлов с тремя ненулевыми индексами. Резкий рост $P(R)$ в интервале $3 \leqslant N \leqslant 4,$ соответствует переходу от одномерного переноса в стопке к трехмерному, в котором доминируют переходы между стопками. Особенность этого перехода состоит в том, что оси $a,$ $b,$ $c$ не ортогональны ($\beta \ne {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$) и при различных значениях трех постоянных решетки $b \ll a \approx c,$ одинаковые значения ${{R}_{n}}$ возникают при различных комбинациях $n$ (рис. 1). Возникающее перемешивание означает, что при достаточно больших $N$ значения ${{R}_{n}}$ плотно заполняют заданный интервал $[{{R}_{1}},{{R}_{2}}],$ $P(R)$ соответствует не регулярной, а стохастической системе [31–33] и переход от одномерной стопки к трехмерной решетке с ростом длины переноса связан с переходом от СПЗ, как состояний с фиксированной длиной переноса, к случайным состояниям. В результате, детерминированное описание следует заменить стохастическим. Переход от регулярной к стохастической модели зависит от заданной точности измерения расстояний ${{R}_{n}}{\text{:}}$ дискретное распределение (17) превращается в непрерывное, и СПЗ при $n \gg 1$ можно заменить огрубленным радиальным распределением, введенным в предыдущем разделе,
(18)
$\tilde {P}(R) = \sum\limits_{s = 1}^{{{N}_{m}}} {{{N}_{s}}{{{\left( {{{{{\xi }_{s}}} \mathord{\left/ {\vphantom {{{{\xi }_{s}}} \pi }} \right. \kern-0em} \pi }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\exp ( - {{\xi }_{s}}{{{\left( {R - {{R}_{s}}} \right)}}^{2}})} ,$(19)
${{N}_{s}} = {{V}^{{ - 1}}}R_{s}^{2}\xi _{s}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}},\,\,\,\,V = 2abc\sin \beta ,$Рис. 1.
Расстояние переноса заряда между узлами (0, 0, 0) и узлами (${{n}_{a}},$ ${{n}_{b}},$ ${{n}_{c}}$) и (${{n}_{a}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ ${{n}_{b}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ ${{n}_{c}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$) в моноклинной решетке кристалла Н2Рс (панели слева и справа соответственно). ${{n}_{b}} = 5.$ Кривые на обеих панелях соответствуют целым значениям ${{n}_{a}}$ от 0 до 15 (снизу вверх).
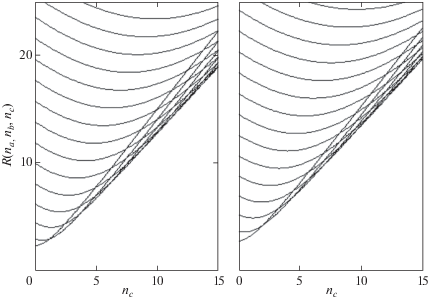
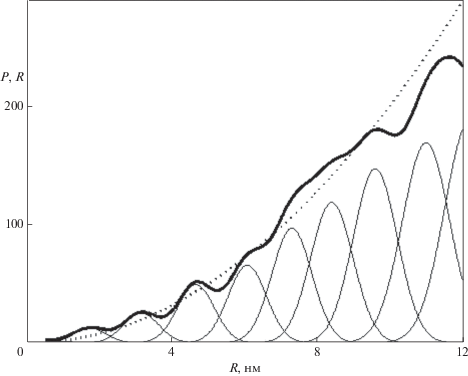
Рис. 2.
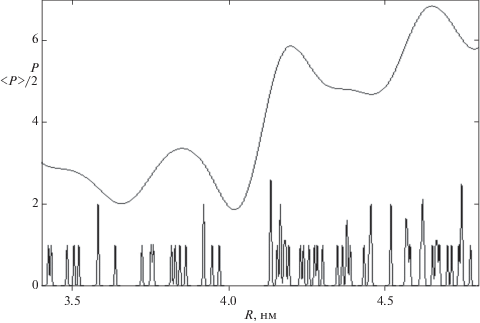
Изменение радиальной плотности СПЗ в решетке Н2Рс при постоянном масштабе огрубления ${{\xi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ в произвольно выбранном интервале расстояний переноса $R \gg a,b,c$ (нм). Внизу: $\xi $ = 104 нм2, где пики с единичной амплитудой соответствуют отдельным узлам, а с удвоенной и большей амплитудой – значениям $R,$ разность которых $ \leqslant {\kern 1pt} 2{{({\xi \mathord{\left/ {\vphantom {\xi \pi }} \right. \kern-0em} \pi })}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$ нм. Сверху: $\xi $ = 102 нм2, кривая суммирует амплитуды пиков в том же интервале.
V. РАДИАЛЬНАЯ ФУНКЦИЯ СТОХАСТИЧЕСКИХ СПЗ
Огрубление вводит дискретный набор параметров $s$-слоев. Чтобы учесть неоднородность слоев, этот набор необходимо дополнить непрерывными функциями координат, характеризующими неоднородность распределения состояний внутри слоев. Введение таких функций основано на гипотезе об универсальности распределения состояний в системах с перемешиванием [38–40]. Обычно предполагается, что распределение является гауссианом, хотя рассматриваются и другие ансамбли [31–33], выбор которых обосновывается дополнительными свойствами рассматриваемой системы. В частности, для сложных ядер считается универсальным энергетическое распределение Вигнера
(20)
$P(x) = \frac{{\pi x}}{2}\exp ({{ - \pi {{x}^{2}}} \mathord{\left/ {\vphantom {{ - \pi {{x}^{2}}} 4}} \right. \kern-0em} 4}),\,\,\,\,x = \left| {{{E}_{j}} - {{E}_{{j{\kern 1pt} '}}}} \right|,$которое описывает также распределение интервалов между частотами нормальных колебаний больших молекул [33, 34] и рассматривает скорее не радиальное, а угловое распределение. Введение подходящего ансамбля позволяет обобщить процедуру огрубления на случай некристаллических и поликристаллических структур, в частности полимерных, для которых нельзя рассчитать решеточную сумму, как это сделано выше в кристаллах Рс. Следуя этой гипотезе, введем непрерывную радиальную функцию
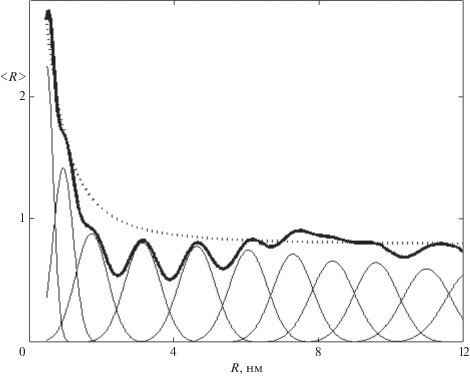
(21)
$\left\langle R \right\rangle = \sum\limits_s {{{{\left( {\frac{{{{\xi }_{s}}}}{\pi }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\exp \left( { - {{\xi }_{s}}{{{(R - {{R}_{s}})}}^{2}}} \right)} ,$показанную на рис. 4. Осцилляции $\left\langle R \right\rangle $ как функции непрерывной переменной $R$ характеризуют неоднородность радиального распределения расстояний переноса внутри слоев, отмеченного на рис. 2. Перемешивание создает локальные максимумы радиальной плотности при значениях ${{R}_{n}},$ равных в масштабе огрубления. Функция (21) воспроизводит наличие трех указанных выше областей с различной структурой слоев. Осцилляции $\left\langle R \right\rangle $ наблюдаются при $s \leqslant 5$ (${{R}_{n}} \leqslant 5$ нм) и постепенно исчезают при $s > 5,$ поскольку распределение стремится к пределу, соответствующему непрерывной среде и определяемому объемом элементарной ячейки (19). Подчеркнем, что в (21), в отличие от (18) не входят плотности состояний ${{N}_{s}}.$ Если распределение узлов в слое предполагается нормальным, вместо совокупности СПЗ как состояний, образующихся при переносе на фиксированный узел, описываемых распределением (18), можно ввести огрубленные состояния, с нормированным распределением по ${{N}_{s}}$ узлам стохастического слоя. Этому распределению соответствует радиальная функция (21) в виде суперпозиции амплитуд узлов, расположенных в шаровом слое. Этот аналог волновой функции характеризует плотность вероятности распределения заряда по узлам шаровых слоев. Таким образом, замена распределения (18) на (21) означает переход к новому вероятностному базису для разложения собственных функций.
VI. ПОТЕНЦИАЛ И СВОБОДНАЯ ЭНЕРГИЯ СТОХАСТИЧЕСКИХ СПЗ
Заменяя $R(n)$ в (6) функцией ${{\left\langle R \right\rangle } \mathord{\left/ {\vphantom {{\left\langle R \right\rangle } R}} \right. \kern-0em} R}$ при том же значении ${{V}_{1}},$ находим потенциал кулоновского взаимодействия (кривая 1 на рис. 5). Начальный участок с сильной связью соответствует $s$ = 1 и 2 ($0.5 \leqslant R \leqslant 1$ нм). Для СПЗ $3 \leqslant s \leqslant 6$ ($1.5 \leqslant R \leqslant 6.5$ нм), кулоновская связь приближается к тепловой энергии и составляет $(1 - 2){{k}_{B}}T$ при 300 К. При дальнейшем росте $R$ потенциальная энергия монотонно растет до нуля. Поскольку разность энергий начальных состояний МЭ и НСПЗ и конечного состояния свободных зарядов не изменяется, энергия активации ионизации равна $\Delta - E{}_{s},$ как и в (2).
Рис. 5.
Модельный потенциал (7) и свободная энергия СПЗ (22) (кривые 1 и 2 соответственно) в кристалле Н2Рс. Пунктиром указаны те же зависимости в пределе однородной среды.
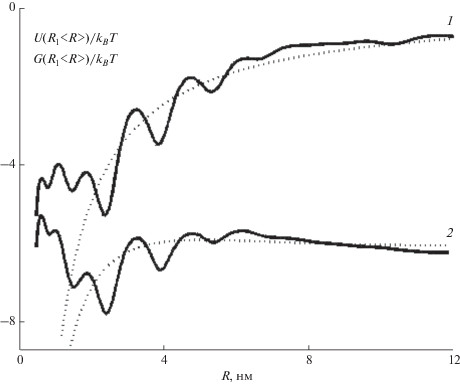
Свободная энергия СПЗ ${{C}_{s}}$ (кривая 2 на рис. 5)
(22)
$G\left( {\left\langle R \right\rangle } \right) = U(\left\langle R \right\rangle ) - {{k}_{B}}T\ln \left( {{{N}_{s}}(R)} \right),$при $s \leqslant 2$ близка к $U(R)$ и более медленно растает при $s$ = 3–4 ($2 \leqslant R \leqslant 2.5$ нм) из-за роста радиальной плотности состояний, которая стремится к пределу (19), равному свободной энергии электронно-дырочной пары в однородной среде. Согласно (22), изменение свободной энергии ионизации МЭ в кристаллах Рс не превышает $(4 - 6){{k}_{B}}T.$ Рост плотности конечных состояний компенсирует кулоновскую связь в МЭ, и члены ряда в (15) экспоненциально уменьшаются. В силу сходимости ряда, (15) сводится к (3) с эффективной константой ${{\gamma }_{{np}}},$ определяемой переходами между СПЗ. Уменьшение свободной энергии согласуется с качественным рассмотрением разделения зарядов в [41].
В динамической теории перекрывание стохастических слоев создает глобальный хаос [38, 40]. В отличие от одномерного кристалла с постоянной плотностью состояний, рост ${{N}_{s}}$ в трехмерном кристалле увеличивает вероятность ионизации МЭ на несколько порядков.
VII. ВЫВОДЫ
1. Вместо рассмотренной ранее феноменологической модели, предполагающей детальное равновесие скоростей ионизации МЭ и рекомбинации ЭДП, предложена кинетическая модель, учитывающая переход МЭ в НСПЗ и последующее обратимое образование СПЗ с растущим расстоянием переноса, много большим всех трех периодов решетки.
2. Модель включает расчет радиальной плотности СПЗ в моноклинной решетке кристаллов Рс.
3. Показано, что вследствие различного масштаба постоянных решетки по ее главным осям, разделение зарядов в процессе перехода МЭ в ЭДП является не эргодическим движением, а движением с перемешиванием, для описания которого необходимо перейти от детерминированного к стохастическому описанию радиальной плотности.
4. Найдена огрубленная радиальная плотность СПЗ в виде суммы гауссианов, относящихся к последовательности радиальных слоев, определяемых их радиусом, толщиной и числом состояний, которая воспроизводит дискретное распределение расстояний переноса в кристаллах Рс в масштабе, большем наименьшего периода решетки. Показано, что разделение зарядов является пространственно неоднородным процессом.
5. Найден огрубленный потенциал кулоновского взаимодействия, свободная энергия и квазистационарные концентрации СПЗ в условиях постоянной оптической накачки.
6. Показано, что ионизация МЭ в кристаллах Рс не описывается в одномерной модели, а должна учитывать уменьшение свободной энергии электронно-дырочной пары вследствие роста числа ее состояний в трехмерной решетке.
7. Предложенная модель огрубленной радиальной плотности СПЗ может быть обобщена для анализа различных механизмов фотоэффекта в неоднородных (в том числе полимерных) материалах, применяемых в органических солнечных элементах.
Список литературы
Usov N.N., Benderskii V.A. // Phys. Stat. Solidi. 1970. V. 37. P. 535.
Бендерский В.А., Белкинд А.И., Федоров М.И., Александров С.Б. // ФТТ. 1972. Т. 14. С. 790.
Liaou H.-C., Chen P.-H., Chang R.P.H., Su W.-F. // Polymer. 2014. V. 6. P. 2784.
Lee C.-H., Lee G.-H., vander Zande A.M., Chen W., li Y., Han M., Cui X., Arefe G., Nuckolis C., Heinz T.F., Guo J., Hone J., Kim P. // Nature Nanotechnol. 2014. V. 9. P. 676.
Elumalai N.K., Uddin A. // Energy Environ. Sci. 2016. V. 9. P. 391.
Ganesamoorthy R., Sathiyan G., Sakthivel P. // Solar energy mater. Solar cells. 2017. V. 161. P. 102.
Trindade A.J., Pereira L. // Int. J. Photoenergy. 2017. N.1D 1364152.
Gaspar H., Figueira F., Pereira L., Mendes A., Viana J.C., Bernardo G. // Materials. 2018. V. 11. P. 2560.
Coropceanu V., Chen X.-K., Wang T., Zheng Z., Bredas J.-L.// Nature Rev. Mater. 2019. V. 4. P. 689.
Fan B., Zhong W., Ying L., Zhang D., Li M., Lin Y., Xia R., Liu F., Yip H.-L., Li H., Ma Y., Brabec C.J., Huang F., Cao Y. // Nature Commun. 2019. V. 10. P. 1038.
Sun H.,Chen F., Chen Z.-K. // Materials Today. 2019. V. 24. P. 94.
Suman, Singh S.P. // J. Mater. Chem. A. 2019. V. 7. P. 22701.
Ferron T., Waldrip M., Pope M., Collins B.A. // J. Mater. Chem. A. 2019. V. 7. P. 536.
Li M., Chen J.-S., Cotlet M. // ACS Energy Lett. 2019. V. 4. P. 2323.
McKeown N.B. // Phthalocyanine Materials. 1998. Cambridge. Univ. Press. Cambridge.
Walter M.G., Rudine A.B., Wamser C.C. // J. Porphyrins Phthalocyanines. 2010. V. 14. P. 759.
Wipps K.W., Mazur U. // J. Porphyrins Phthalocyanines. 2012. V. 16. P. 273.
Zou T., Wang X., Ju H., Zhao L., Guo T., Wu W., Wang H. // Crystals. 2018. V. 8. P. 1.
Agranovich V.M. // Excitations in Organic Solids. 2008. AIP Press. N.Y.
Bondarev I.V., Popescu A., Younts R.A., Hoffman B., McAfee T., Dougherty D.B., Gundogdu K., Ade H.W. // Appl. Phys. Lett. 2016. V. 109. P. 213302.
Hiramoto M., Kubo M., Shinmura Y., IShiyama N., Kaji T., Sakai K., Ohno T., Izaki M. // Elecronics. 2014. V. 3. P. 351.
Lalov I.J., Warns C., Reineker P. // New J. Phys. 2008. V. 10. № 085006.
Guan Y.-S., Zhang Z., Pan J., Jan Q., Ren S. // J. Mater. Chem. C. 2017. P. 12338.
Usman R., Khan A., Wang M., Luo Y., Sun W., Sun H., Du C., He N. // Crystal Growth Design. 2018. V. 18. P. 6001.
Merrifield R.E. // J. Chem. Phys. 1961. V. 34. P. 1835.
Бендерский В.А., Блюменфельд Л.А., Попов Д.А. // Журн. Структурн. Химии. 1966. Т. 7. С. 370.
Zoos Z.G. // Annu. Rev. Phys. Chem. 1974. V. 25. P. 121.
Hill I.G., Kahn A., Soos Z.G., Pascal R.A. // Chem. Phys. Lett. 2000. V. 327. P. 181.
Бендерский В.А., Кац Е.И. // Письма в ЖЭТФ. 2015. Т. 101. С. 17.
Бендерский В.А., Кац Е.И. // ЖЭТФ. 2018. Т. 127. С. 566.
Mehta M.L. Random Matrices. 1968. Academic N.Y. Press.
Papenbrock T., Weidenmuller H.A. // Rev. Mod. Phys. 2007. V. 79. P. 997.
Rodrigues K.R., Shah S., Williams S.M., Teters-Kennedy S., Coe J.V. // J. Chem. Phys. 2004. V. 121. P. 8671.
Бендерский В.А., Гак Л.Н., Кац Е.И. // ЖЭТФ. 2009. Т. 135. С. 176.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Ovchinnikov A.A., Ovchinnikova M.Y. // Adv. Quant. Chem. 1982. V. 16. P. 161.
Benderskii V.A., Benderskii A.V. Laser Electrochemistry of Intermediates. 1995. CRCPress. N.Y.
Заславский Г.М. Стохастичность динамических систем. М.: Наука, 1984.
Вишик А.М., Корнфельд И.П., Синай Я.Г. Общая эргодическая теория динамических систем. Современные проблемы математики. 1985. Т. 1. ВИНИТИ. Москва.
Chirikov B.V. // Phys. Rep. 1979. V. 52. P. 527.
Бендерский В.А., Кац Е.И. // Химия высоких энергий. 2020. Т. 54. № 3. С. 192.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий