1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 123, № 5, 2022

Физика металлов и металловедение, 2022, T. 123, № 5, стр. 462-468

К теории взаимной диффузии в трехкомпонентных сплавах. Концентрационные зависимости коэффициентов, определяющих кинетику процесса

Г. В. Сергеев a, В. А. Макарова a, Р. З. Кахидзе a, А. В. Назаров a, b, *

a Национальный Исследовательский Ядерный Университет, МИФИ
115487 Москва, Каширское ш., 31, Россия

b Институт теоретической и экспериментальной физики им. А.И. Алиханова Национального исследовательского центра “Курчатовский институт”
117218 Москва, Большая Черемушкинская ул., 25, Россия

* E-mail: avn46@mail.ru

Поступила в редакцию 27.10.2021
После доработки 11.01.2022
Принята к публикации 12.01.2022

Полный текст (PDF)

Аннотация

Проведены иллюстративные расчеты концентрационных зависимостей коэффициентов взаимной диффузии и коэффициентов, определяющих вклады начальных и граничных условий для различных компонентов сплава в распределение концентраций в диффузионной зоне. Проведенный анализ упомянутых зависимостей показывает, что кинетика перераспределения компонентов определяется главным образом медленно диффундирующим компонентом, что отличает результаты развиваемого подхода от предсказаний теорий обобщающих подход Даркена.

Ключевые слова: взаимная диффузия, многокомпонентные сплавы, теория, коэффициенты взаимной диффузии, “замедленная” диффузия

ВВЕДЕНИЕ

Большинство применяемых в промышленности сплавов имеют многокомпонентный состав и многофазную структуру. Прогнозирование формирования структуры при изготовлении изделий из сплавов и ее деградации в условиях эксплуатации возможно только при адекватном понимании и умении описывать диффузионные процессы в таких системах [1–6]. Однако особенности диффузии в многокомпонентных сплавах не до конца ясны, и не всегда понятны причины этих особенностей [7‒9]. В частности, это касается замедленной диффузии в высокоэнтропийных сплавах [9].

В работе [10] подход, который ранее был развит для бинарных систем [11–19], обобщен на случай трехкомпонентных сплавов, разработан его математический аппарат, получены выражения для коэффициентов взаимной диффузии и коэффициентов, определяющих вклады начальных и граничных условий для различных компонентов сплава в распределение концентраций в диффузионной зоне.

В предлагаемой вниманию работе проведены расчеты концентрационных зависимостей упомянутых коэффициентов, построены иллюстрирующие эти зависимости графики, и на основе результатов проведeн анализ особенностей взаимной диффузии в трехкомпонентных сплавах и возможные причины замедления диффузии в таких системах.

РЕШЕНИЯ СИСТЕМЫ ДИФФУЗИОННЫХ УРАВНЕНИЙ ДЛЯ ТРЕХ КОМПОНЕНТОВ И ВАКАНСИЙ [10]

В работе [10] в качестве базовых были использованы уравнения для потоков вакансий и атомов в тройной системе, полученные методом дырочного газа Гурова [3, 4]. После подстановки выражений для потоков в уравнения непрерывности, получена система четырех нелинейных взаимосвязанных уравнений, которая линеаризована аналогично тому, как это было сделано в случае описания взаимной диффузии в бинарных системах в работе [13]. При этом использовали условие малости градиентов концентраций, т.к. уравнения для потоков были получены в [3, 4] с применением таких же условий, и представление концентраций в виде суммы двух слагаемых:

(1)
$\begin{gathered} {{c}^{i}}\left( {x + {{\xi }},~t + {{\tau }}} \right) = {{c}_{i}}\left( {x,t} \right) + ~{{u}^{i}}\left( {x,t,{{\xi }},{{\tau }}} \right), \\ {{c}_{v}}\left( {x + {{\xi }},~t + {{\tau }}} \right) = c\left( {x,t} \right) + v\left( {x,t,{{\xi }},{{\tau }}} \right),~ \\ \end{gathered} $
где cv – концентрация вакансий, ci – концентрации компонентов i = 1, 2, 3, $0 \leqslant {{\xi }} \leqslant l,$ ${{\tau }} < {{t}_{1}}.$

Систему линеаризованных уравнений для ${{u}^{i}}$ и $v$ (см. (5) в [10]) решали, используя функции Грина для параболических уравнений [20], что позволило записать искомые функции в виде рядов (детали см. [13]):

(2)
${{u}^{i}} = \sum\limits_{n = 1}^\infty {{{\varphi }}_{n}^{i}\left( {{\tau }} \right)\sin \left( {{{{{\lambda }}}_{n}}{{\xi }}} \right)} ;\,\,\,\,v = \sum\limits_{n = 1}^\infty {{{{{\varphi }}}_{n}}\left( {{\tau }} \right)\sin \left( {{{{{\lambda }}}_{n}}{{\xi }}} \right)} ,$
где ${{{{\lambda }}}_{n}} = {{{{\pi }}n} \mathord{\left/ {\vphantom {{{{\pi }}n} l}} \right. \kern-0em} l}.$

Используя ортогональность ${\text{sin}}\left( {{{{{\lambda }}}_{n}}{{\xi }}} \right),$ систему диффузионных уравнений в [10] преобразовали к системе интегральных уравнений для ${{\varphi }}_{n}^{i}\left( {{\tau }} \right)$ и ${{{{\varphi }}}_{n}}\left( {{\tau }} \right).$ Эта система уравнений решена с помощью преобразования Лапласа. Получающееся при решении характеристическое уравнение ((9) в [10])) имеет корни, которые определяют зависимость концентраций компонентов сплава и вакансий от времени. Причем распределение концентраций компонентов сплава в диффузионной зоне с точностью до членов более высокого порядка по концентрации вакансий определяются двумя коэффициентами взаимной диффузии, которые являются корнями квадратного уравнения с коэффициентами:

(3)
$\begin{gathered} {{B}_{q}} = - ~\frac{{\left( {{{c}_{2}}{{D}_{2}} + {{c}_{3}}{{D}_{3}}} \right){{D}_{1}} + \left( {{{c}_{1}}{{D}_{1}} + {{c}_{3}}{{D}_{3}}} \right){{D}_{2}}}}{{\left( {{{c}_{1}}{{D}_{1}} + {{c}_{2}}{{D}_{2}} + {{c}_{3}}{{D}_{3}}} \right)}}\,\,~ - \\ - \,\,~\frac{{\left( {{{c}_{1}}{{D}_{1}} + {{c}_{2}}{{D}_{2}}} \right){{D}_{3}}}}{{\left( {{{c}_{1}}{{D}_{1}} + {{c}_{2}}{{D}_{2}} + {{c}_{3}}{{D}_{3}}} \right)}}, \\ {{C}_{q}} = \frac{{{{D}_{1}}{{D}_{2}}{{D}_{3}}~~}}{{\left( {{{c}_{1}}{{D}_{1}} + {{c}_{2}}{{D}_{2}} + {{c}_{3}}{{D}_{3}}} \right){{S}_{D}}}}. \\ \end{gathered} $

Тогда формулы для этих корней имеют вид:

(4)
${{p}_{3}} = - {{\lambda }}_{n}^{2}{{D}^{ + }},\,\,\,{{D}^{ + }} = \frac{{ - {{B}_{q}}}}{2} + {{\left[ {{{{\left( {\frac{{{{B}_{q}}}}{2}} \right)}}^{2}} - {{C}_{q}}} \right]}^{{\frac{1}{2}}}};$
(5)
${{p}_{4}} = - {{\lambda }}_{n}^{2}{{D}^{ - }},\,\,\,{{D}^{ - }} = \frac{{ - {{B}_{q}}}}{2} - {{\left[ {{{{\left( {\frac{{{{B}_{q}}}}{2}} \right)}}^{2}} - {{C}_{q}}} \right]}^{{\frac{1}{2}}}},$
где ${{D}_{1}},~{{D}_{2}},~{{D}_{3}}$ – коэффициенты самодиффузии, а ${{\varphi }}_{n}^{1}\left( p \right)$ с такой же точностью определяется выражением:
(6)
$\begin{gathered} {{\varphi }}_{n}^{1}\left( p \right) = {{\Phi }}_{n}^{1}\left( p \right)\left[ {M_{1}^{{1 + }}\frac{1}{{p + {{\lambda }}_{n}^{2}{{D}^{ + }}}} + M_{1}^{{1 - }}\frac{1}{{p + {{\lambda }}_{n}^{2}{{D}^{ - }}}}} \right] + \\ + \,\,~{{\Phi }}_{n}^{2}\left( p \right)\left[ {M_{2}^{{1 + }}\frac{1}{{p + {{\lambda }}_{n}^{2}{{D}^{ + }}}} + ~M_{2}^{{1 - }}\frac{1}{{p + {{\lambda }}_{n}^{2}{{D}^{ - }}}}} \right] + \\ + \,\,{{\Phi }}_{n}^{3}\left( p \right)\left[ {M_{3}^{{1 + }}\frac{1}{{p + {{\lambda }}_{n}^{2}{{D}^{ + }}}} + M_{3}^{{1 - }}\frac{1}{{p + {{\lambda }}_{n}^{2}{{D}^{ - }}}}} \right], \\ \end{gathered} $
где

$\begin{gathered} M_{1}^{{1 + }} = - ~\frac{{{{D}_{1}}{{z}_{1}}{{c}_{1}}\left( {{{D}^{ + }} - {{D}_{2}}} \right)\left( {{{D}^{ + }} - {{D}_{3}}} \right)}}{{{{D}^{ + }}\left( {\hat {D} - {{D}^{ + }}} \right)\left( {{{D}^{ + }} - {{D}^{ - }}} \right)\left( {{{D}^{ + }} - {{D}_{1}}} \right)}}, \\ M_{1}^{{1 - }} = \frac{{{{D}_{1}}{{z}_{1}}{{c}_{1}}\left( {{{D}^{ - }} - {{D}_{2}}} \right)\left( {{{D}^{ - }} - {{D}_{3}}} \right)}}{{{{D}^{ - }}\left( {\hat {D} - {{D}^{ - }}} \right)\left( {{{D}^{ + }} - {{D}^{ - }}} \right)\left( {{{D}^{ - }} - {{D}_{1}}} \right)}}, \\ M_{2}^{{1 + }} = - \frac{{{{D}_{2}}{{z}_{1}}{{c}_{1}}\left( {{{D}^{ + }} - {{D}_{3}}} \right)}}{{{{D}^{ + }}\left( {\hat {D} - {{D}^{ + }}} \right)\left( {{{D}^{ + }} - {{D}^{ - }}} \right)}}, \\ M_{2}^{{1 - }} = ~\frac{{{{D}_{2}}{{z}_{1}}{{c}_{1}}\left( {{{D}^{ - }} - {{D}_{3}}} \right)}}{{{{D}^{ - }}\left( {\hat {D} - {{D}^{ - }}} \right)\left( {{{D}^{ + }} - {{D}^{ - }}} \right)}}, \\ M_{3}^{{1 + }} = - \frac{{{{D}_{3}}{{z}_{1}}{{c}_{1}}\left( {{{D}^{ + }} - {{D}_{2}}} \right)}}{{{{D}^{ + }}\left( {\hat {D} - {{D}^{ + }}} \right)\left( {{{D}^{ + }} - {{D}^{ - }}} \right)}}, \\ M_{3}^{{1 - }} = \frac{{{{D}_{3}}{{z}_{1}}{{c}_{1}}\left( {{{D}^{ - }} - {{D}_{2}}} \right)}}{{{{D}^{ - }}\left( {\hat {D} - {{D}^{ - }}} \right)\left( {{{D}^{ + }} - {{D}^{ - }}} \right)}}. \\ \end{gathered} $
${{\Phi }}_{n}^{i}\left( p \right) = ~{{\varphi }}_{n}^{i}\left( 0 \right) + \,\,~\frac{{2{{\pi }}n{{D}_{i}}}}{{{{l}^{2}}}}u_{{0l}}^{i}\left( p \right),$

$u_{{0l}}^{i}\left( p \right)$ – образ Лапласа функции

$u_{{0l}}^{i}\left( {{\tau }} \right) = {{u}^{i}}\left( {0,{{\tau }}} \right) - {{\left( { - 1} \right)}^{n}}{{u}^{i}}\left( {l,{{\tau }}} \right),$

определяющей в решении диффузионного уравнения для компонента i вклад граничных условий первого рода, заданных на границах интервала l.

Чтобы получить выражение для ${{\varphi }}_{n}^{2}\left( p \right)$ достаточно в ${{\varphi }}_{n}^{1}\left( p \right)~$сделать замену индексов 1 → 2; 2 → 3; 3 → 1; а для ${{\varphi }}_{n}^{3}\left( p \right)$ соответственно 1 → 3; 3 → 2; 2 → 1.

Таким образом, изменение со временем концентраций компонентов сплава определяется двумя коэффициентами ${{D}^{ + }}$ и ${{D}^{ - }}.$ Причем вид концентрационных кривых зависит не только от них, но и от 6 оставшихся элементов матрицы M1 (см. (6)).

КОНЦЕНТРАЦИОННЫЕ ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ ${{D}^{ + }}$ И ${{D}^{ - }}$ И ЭЛЕМЕНТОВ МАТРИЦЫ M1

Коэффициенты ${{D}^{ + }}$ и ${{D}^{ - }}$ и элементы матрицы M1 (6) имеют сложную зависимость от концентраций компонентов сплава, поэтому были проведены иллюстративные расчеты таких зависимостей, и построены графики при некоторых значениях коэффициентов Di, которые для простоты предполагались не зависящими от концентраций величинами, что нередко используется во многих теоретических работах. Так, на рис. 1 и 2 приведены зависимости ${{D}^{ + }}$ и ${{D}^{ - }}$ при различных соотношении между коэффициентами D1, D2, D3.

Рис. 1.

Зависимость коэффициентов D+ (а) и D– (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 3 : 2 : 1. Результаты для эквиатомного состава (с1 = с2 = с3 = 1/3), D+ = 2.434, D– = 1.232.

Рис. 2.

Зависимость коэффициентов D+ (а) и D– (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 10 : 4 : 1. Для эквиатомного состава (с1 = с2 = с3 = 1/3), D+ = 5.827, D– = 1.373.

Из результатов, приведенных на рис. 1, 2, следует, что при различных значениях концентраций ${{D}^{ + }}$ изменяется в интервале от величины среднего из коэффициентов самодиффузии до значения наибольшего из коэффициентов, а ${{D}^{ - }}$ в интервале от значения наименьшего из коэффициентов самодиффузии до величины среднего из коэффициентов самодиффузии. Т.е. слагаемые, расположенные в правом столбце уравнения (6), являются наиболее медленно меняющимися со временем. Кроме того, эти коэффициенты имеют существенно меньшие значения, чем при любых, но линейных зависимостях диагональных коэффициентов, как например в теориях, являющихся обобщениями даркеновского подхода на трехкомпонентные системы [4]. Причем, эти отклонения проявляются максимальным образом при эквиатомном составе сплава.

Для более детального анализа полученных зависимостей коэффициентов ${{D}^{ + }}$ и ${{D}^{ - }}$ были рассчитаны их величины при постоянной концентрации одного из компонентов. Результаты приведены на рис. 3.

Рис. 3.

Зависимость коэффициентов D+ и D– от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 10 : 4 : 1 при различных постоянных значениях компонента с3.

Все полученные выражения: ${{\varphi }}_{n}^{i}\left( p \right),~$ имеют такую же структуру, как и в случае двухкомпонентной системы (см. [13]). Однако, коэффициенты, которые стоят при функциях от $p,$ определяющих временную зависимость, имеют гораздо более сложный вид и их не удается выразить через ${{D}_{i}},{{D}_{V}}$ так, чтобы поучились обозримые выражения. Поэтому далее на рис. 4–7 представлены графики, иллюстрирующие зависимость элементов матрицы M1 от концентраций при тех же соотношениях между коэффициентами самодиффузии что и ранее. Причем приводятся графики только для элементов матриц, имеющих старший порядок по концентрации вакансий. Вначале на рис. 4 и рис. 6 представлены графики для элементов матрицы M1 (6), определяющих вклад в зависимость концентрации первого компонента в диффузионной зоне от координат и времени слагаемых, определяемых начальными и граничными условиями для первого компонента (см. (6)), а затем (рис. 5, 7) для второго.

Рис. 4.

Зависимость коэффициентов $M_{1}^{{1 + }}$ (а) и $M_{1}^{{1 - }}$ (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 3 : 2 : 1. Для эквиатомного состава (с1 = с2 = с3 = 1/3), $M_{1}^{{1 + }} = 0.564,$ $M_{1}^{{1 - }}$ = 0.102.

Рис. 5.

Зависимость коэффициентов $M_{2}^{{1 + }}$ (а) и $M_{2}^{{1 - }}$ (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 3 : 2 : 1. Для эквиатомного состава (с1 = с2 = с3 = 1/3) $M_{2}^{{1 + }} = 0.490,$ $M_{2}^{{1 - }}$ = 0.156.

Рис. 6.

Зависимость коэффициентов $M_{1}^{{1 + }}$ (а) и $M_{1}^{{1 - }}$ (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 10 : 4 : 1. Для эквиатомного состава (с1 = с2 = с3 = 1/3), $M_{1}^{{1 + }} = 0.543,$ $M_{1}^{{1 - }}$ = 0.124.

Рис.7.

Зависимость коэффициентов $M_{2}^{{1 + }}$ (а) и $M_{2}^{{1 - }}$ (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 10 : 4 : 1. Для эквиатомного состава (с1 = с2 = с3 = 1/3), $M_{2}^{{1 + }} = 0.496,$ $M_{2}^{{1 - }} = 0.163.$

Следует отметить, что коэффициенты имеют одинаковый порядок величин. Причем, в некоторой области изменения концентраций элементы правого столбца матрицы M1 (6), определяющие вклад медленно меняющихся слагаемых (зависящих от ${{D}^{ - }}$), имеют значения превышающие величины элементов среднего столбца этой матрицы (зависящих от ${{D}^{ + }}$). Т.е. в этой области концентраций будет преобладать медленное изменение концентрации первого компонента и других со временем.

На рис. 6, 7 приведены зависимости аналогичных элементов матрицы для другого соотношения коэффициентов самодиффузии.

Из приведенных данных видно, что они имеют очень близкий характер и несколько различаются количественно, но не качественно. Дополнительно проведены расчеты ${{D}^{ + }}$ и ${{D}^{ - }}$ при двух соотношениях между коэффициентами самодиффузии таких, что их средние значения совпадают (рис. 8 и 9).

Рис. 8.

Зависимость коэффициентов D+ (а) и D– (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 9 : 5 : 1. Для эквиатомного состава (с1 = с2 = с3 = 1/3), D+ = 6.477, D– = 1.389.

Рис. 9.

Зависимость коэффициентов D+ (а) и D– (б) от концентраций при соотношении коэффициентов самодиффузии D1 : D2 : D3 как 6 : 5 : 4. Для эквиатомного состава (с1 = с2 = с3 = 1/3), D+ = 5.515, D– = 4.352.

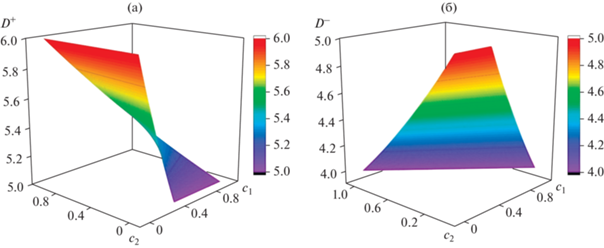
Анализ приведенных на этих рисунках результатов показывает, что чем больше различие коэффициентов самодиффузии в системе при их одинаковом среднем значении, тем меньше величина коэффициента ${{D}^{ - }},$ и тем более выраженными будут эффекты замедления взаимной диффузии при эквиатомном составе сплава и ряде других составов. Кроме того, вклад таких слагаемых при указанных условиях будет также больше, что следует из величин компонент матрицы М.

ЗАКЛЮЧЕНИЕ

Таким образом в работе изучены концентрационные зависимости коэффициентов диффузии, ответственных за перераспределение компонентов сплава в диффузионной зоне, а также за кинетику любых диффузионных превращений в таких системах. Как следует из полученных ранее уравнений, а также из приведенных на рисунках иллюстраций, упомянутые коэффициенты нелинейным образом зависят от концентраций и коэффициентов самодиффузии. Причем больший из этих коэффициентов может принимать значения в интервале от среднего коэффициента самодиффузии, до максимального, а меньший – от наименьшего до среднего. Предварительные результаты свидетельствуют, что в трехкомпонентном сплаве взаимная диффузия будет происходить медленнее по сравнению с предсказаниями теорий, обобщающих подход Даркена [4], и в наибольшей степени это различие будет проявляться для сплавов эквиатомного состава и при увеличении отличия между коэффициентами самодиффузии. Другими словами, следует ожидать, что замедленная диффузия ‘sluggish diffusion’ будет наблюдаться в тех сплавах, где максимальный и минимальный коэффициенты самодиффузии различаются в пять раз (приблизительно) и более.

Авторы хотели бы отметить финансовую поддержку Национального исследовательского ядерного университета МИФИ “Проект академического превосходства” (Контракт № 02.a03.21.0005).

Список литературы

  1. Shewmon P.G. Diffusion in Solids. Warrendale, PA, McGraw-Hill Book Comp, 1989. 244 p.

  2. Маннинг Дж. Кинетика диффузии атомов в кристаллах. М.: Мир, 1971. 277 с.

  3. Боровский И.Б., Гуров К.П., Марчукова И.Д., Угасте Ю.Э. Процессы взаимной диффузии в сплавах. М.: Наука, 1973. 360 с.

  4. Гуров К.П., Карташкин Б.А., Угасте Ю.Э. Взаимная диффузия в многокомпонентных металлических системах. М.: Наука, 1981. 350 с.

  5. Mehrer H. Diffusion in solids – Fundamentals, methods, materials, diffusion-controlled processes. Textbook, Springer Series in Solid-State Sciences. V. 155. Springer-Verlag, Berlin Helderberg, 2007. 651 p.

  6. Paul A., Laurila T., Vuorinen V., Divinski S.V. Thermodynamics, Diffusion and the Kirkendall Effect in Solids. Springer Cham. Heidelberg, N.Y., Dordrecht London, 2014. 530 p.

  7. Axel van de Walle, Mark Asta. High-throughput calculations in the context of alloy design // MRS Bulletin. V. 44, Issue 4. Apr-2019. P. 252–256.

  8. George E.P., Raabe D., Ritchie R.O. High-entropy alloys // Nature Reviews Materials. V. 4. 2019. P. 515–534.

  9. Divinski S.V., Pokoev A., Eesakkiraja N., Paul A. A mystery of ‘sluggish diffusion’ in high-entropy alloys: the truth or a myth? // Diffusion Foundations. 2018. V. 17. P. 69–104. https://doi.org/10.4028/www.scientific.net/DF.17.69

  10. Назаров А.В. К теории взаимной диффузии в трехкомпонентных сплавах // ФММ. 2022. Т. 123. № 5. С. 1–7.

  11. Назаров А.В., Гуров К.П. Микроскопическая теория взаимной диффузии в бинарной системе с неравновесными вакансиями // ФММ. 1972. Т. 34. № 5. С. 936–941.

  12. Назаров А.В. Нескомпенсированный поток вакансий и эффект Киркендалла // ФММ. 1973. Т. 35. № 3. С. 645–649.

  13. Назаров А.В., Гуров К.П. Кинетическая теория взаимной диффузии в бинарной системе. Концентрация вакансий при взаимной диффузии // ФММ. 1974. Т. 37. № 3. С. 496–503.

  14. Назаров А.В., Гуров К.П. Кинетическая теория взаимной диффузии в бинарной системе. Влияние концентрационной зависимости коэффициентов самодиффузии на процесс взаимной диффузии // ФММ. 1974. Т. 38. № 3. С. 486–492.

  15. Назаров А.В., Гуров К.П. Кинетическая теория взаимной диффузии в бинарной системе. Эффект Киркендалла // ФММ. 1974. Т. 38. № 4. С. 689–695.

  16. Назаров А.В., Гуров К.П. Учет неравновесных вакансий в феноменологической теории взаимной диффузии // ФММ. 1978. Т. 45. № 4. С. 885–887.

  17. Мусин К.С., Назаров А.В., Гуров К.П. Влияние упорядочения на взаимную диффузию в бинарных сплавах // ФММ. 1987. Т. 63. № 2. С. 267–277.

  18. Nazarov A.V., Mikheev A.A. Effect of Elastic Stress Field on Diffusion // Defect and Diffusion Forum. 1997. V. 143–147. P. 177–185.

  19. Назаров А.В. Метод дырочного газа К.П. Гурова и альтернативная теория взаимной диффузии // Физика и химия обработки материалов. 2018. № 2. С. 48–62.

  20. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1972. 736 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал