1. На главную
  2. Электронные версии
  3. Генетика
  4. T. 58, № 1, 2022

Генетика, 2022, T. 58, № 1, стр. 99-115

Эволюция хищника в модели взаимодействующих видов: к вопросу о существовании полиморфизма по размеру помета в естественных популяциях песцов

О. Л. Жданова 1, *, Г. П. Неверова 1, Е. Я. Фрисман 2

1 Институт автоматики и процессов управления Дальневосточного отделения Российской академии наук
690041 Владивосток, Россия

2 Институт комплексного анализа региональных проблем Дальневосточного отделения Российской академии наук
679016 Биробиджан, Россия

* E-mail: axanka@iacp.dvo.ru

Поступила в редакцию 16.03.2021
После доработки 21.04.2021
Принята к публикации 25.05.2021

Полный текст (PDF)

Аннотация

Предложена эколого-генетическая модель сообщества “хищник–жертва”, в которой приспособленность хищника определяется генетически одним диаллельным плейотропным локусом. Рассматривается аутосомный локус диплоидной популяции. Различные генотипы хищника, отличаясь по репродуктивному потенциалу, неодинаково приспособлены и к ограничению по пищевым ресурсам, в результате приспособленность генотипа хищника определяется не только его собственным генотипом, но и численностью жертвы. Модель представлена уравнениями с дискретным временем, что позволяет учитывать ярко выраженную цикличность жизненного цикла видов, составляющих сообщество. Данная работа продолжает наши предыдущие исследования, посвященные моделированию эволюции локальной популяции и объяснению существующего генетического разнообразия по размеру помета в различных (естественных и искусственных) популяциях песцов Alopex lagopus. Явное включение в модель популяционной динамики жертвы и рассмотрение полного сообщества позволяют оценить возможности поддержания полиморфизма в популяциях песца в более реалистичных условиях. Проведенное исследование показывает, что направление эволюции популяции хищника, как и в более простых моделях, в целом определяется взаимным расположением приспособленностей его генотипов, при этом характер динамики взаимодействующих видов определяется уже набором параметров, характеризующих репродуктивные способности жертвы и хищника, а также характеристиками межвидового взаимодействия. Вместе с тем устойчивое поддержание полиморфизма у хищника возможно даже в отсутствие сверхдоминирования, когда значительные по амплитуде колебания обилия жертвы меняют направление отбора в популяции хищника. При этом различная динамика генетического состава хищника может привести к смене динамического режима в популяции жертвы.

Ключевые слова: эволюция, естественный отбор, динамика сообщества, хищник–жертва, теоретическая популяционная генетика, полиморфизм.

Появившиеся в начале прошлого столетия классические работы А. Лотки [1] и В. Вольтерры [2], рассматривающие динамику взаимодействующих видов, радикально изменили принципы моделирования в экологии. Предложенная ими концепция и ее развитие, реализованное во множестве работ (которые невозможно более-менее полно охарактеризовать в рамках одного обзора (например, [3–7])), по сути сформировали новую теорию математической экологии [8], которая гармонично объединила в себе разработанные ранее принципы внутривидовой регуляции ([9, 10] и др.) и межвидовых взаимодействий: от простейших двухвидовых сообществ “хищник–жертва” и “паразит–хозяин” до целых пищевых цепочек. Пионерские работы [11–15], объединившие популяционно-генетическую теорию [16–18] и концепцию межвидового взаимодействия [1, 2], долгое время не получали широкого внимания и развития, поскольку считалось, что экологические и эволюционные процессы имеют разные временные шкалы [19] и результирующая микроэволюция не влияет на экологическую динамику. При всей сложности создаваемых моделей межвидового взаимодействия долгое время в традиционной экологии не выделяли внутривидовые генетические вариации популяций, составляющих сообщество [3, 4, 20, 21].

Благодаря росту количества экспериментальных работ и наблюдений, подтверждающих то, что биологическая эволюция особенностей жизненного цикла организмов может происходить в масштабе времени, аналогичном динамике их популяций [22–24], относительно недавно появилось понятие “быстрой эволюции” (Rapid Evolution). Это неизбежно привело к пониманию того, что быстрая эволюция может формировать экологическую динамику взаимодействующих видов [25] и необходимо учитывать этот факт при моделировании динамики сообществ.

В результате интерес к эколого-генетическому подходу в моделировании взаимодействующих видов значительно вырос. К настоящему времени синтез эволюционного и экологического подходов представляет собой широкий спектр теоретических и практических работ, однако новая синтетическая теория развивается преимущественно на основе упрощенных моделей эволюции, детально не рассматривающих генетическую динамику. Как правило, моделируется эволюция полигенных непрерывно распределенных признаков (или количественных признаков [26]) (например, [21, 27–31], а также эволюция клональных систем хищник–жертва (часто эквивалентных гаплоидным генетическим моделям), в которых особи имеют отдельные дискретные значения признаков и идеальное наследование фенотипов, нарушаемое редкими мутациями [21, 27, 30, 32]. Относительно недавно появилась серия работ, моделирующих генетически неоднородное сообщество “хищник–жертва”, в котором один из видов [33–35] или оба [36–38] состоят из двух генетически различимых групп. Этот подход также не предполагает детального описания механизма наследования признаков, при этом популяция одного из взаимодействующих видов формально делится на две группы (называемые генетически различимыми), каждая из которых описывается отдельным уравнением.

Прямой перенос популяционно-генетических уравнений, не упрощающих принципы менделевского наследования, в модели экологического сообщества, реализованный в ранних работах В.А. Костицина [11] и Д. Пиментеля [12, 13], как правило, не используется, и работы, продолжающие именно это направление, крайне редки (например, [39–41]). Причина непопулярности монолокусных моделей, по-видимому, связана с укоренившимся представлением о полигенном контроле фенотипических признаков, а увеличение количества рассматриваемых локусов значительно усложняет модель и быстро лишает возможности адекватно интерпретировать результаты моделирования.

Тем не менее оказалось, что монолокусное наследование важнейших признаков жизненного цикла животных наблюдается в природе. В частности, Т.И. Аксенович с соавт. [42] показали, что механизм наследования размера помета у песцов Alopex lagopus соответствует простейшей Менделевской однолокусной модели. Кроме того, песец представляет собой интересный пример вида, участвующего в различных сообществах, взаимодействующих по принципу “хищник–жертва”. Заметим, что естественные популяции песца, населяющие прибрежные и континентальные территории, радикально отличаются по своей репродуктивной стратегии. Прибрежные песцы питаются морскими птицами, рыбой, тюленями и морскими беспозвоночными [43]. Из года в год наблюдаются лишь очень небольшие колебания доступности этих ресурсов. Каждый год прибрежные песцы производят приплод небольшого размера [44]. Континентальные песцы питаются мелкими грызунами, главным образом полевками, численность которых характеризуется циклическими колебаниями [45]. В голодные годы популяции континентальных песцов демонстрируют крайне низкий репродуктивный уровень, а в годы с обильной пищей (когда в популяциях жертвы наблюдается подъем численности) резко увеличивают свою плодовитость [46–48]. Это позволило предположить, что прибрежные песцы однородны по размеру помета, а континентальные неоднородны и представлены особями с разной потенциальной плодовитостью. Полиморфизм по размеру помета наблюдается и у песцов, которых разводят в фермерских звероводческих хозяйствах. Проведенный в работе [42] комплексный сегрегационный анализ типа наследования размера помета в расширенной генеалогии фермерских песцов подтвердил, что данный признак является аутосомным женским признаком, а его наследование можно описать в рамках смешанной модели с основным геном и контролем малого размера помета по рецессивному типу.

В данной работе мы предлагаем эколого-генетическую модель сообщества “хищник–жертва”, которая в явном виде описывает Менделевский механизм наследования одного из признаков жизненного цикла хищника, его репродуктивный уровень. При моделировании мы ориентировались на сообщество “песец–мышевидные грызуны”, представляющее собой пример межвидового взаимодействия типа “хищник–жертва”, при описании которого важно учитывать не только экологические переменные, но и генетическую структуру хищника.

Поскольку один из важнейших признаков жизненного цикла песца – размер помета определяется генетически одним диаллельным локусом, использование однолокусной диаллельной модели наследования в данном случае вполне оправдано. Более того, при ограниченности ресурсов питания (в данном случае при малой численности мышевидных грызунов – “жертвы”) в больших и малых пометах песцов выживаемость щенков различается, поэтому рассматриваемый локус определяет не только репродуктивный уровень, но и выживаемость потомства в популяции песцов, т.е. его можно считать плейотропным. Вместе с тем выживаемость песцов, особенно в больших пометах, будет существенно зависеть от уровня обеспеченности кормом – от численности “жертвы” – мышевидных грызунов в данном случае. Для моделирования такой ситуации вместо постоянных приспособленностей генотипов, используемых в классических работах [11–13], мы введем функциональную зависимость приспособленностей генотипических групп хищника от численности жертвы. В соответствии с этим текущая абсолютная приспособленность генотипа хищника, представляющая собой произведение рождаемости и выживаемости, определяется теперь не только его собственным генотипом, но и численностью жертвы.

Данная работа продолжает наши предыдущие исследования [49, 50], посвященные моделированию механизма дифференциации репродуктивных стратегий в естественных популяциях песцов. В предыдущих работах мы изучали динамику генетического состава локальной популяции, учитывая циклы кормовой базы с помощью периодически изменяющихся параметров. Такое упрощение позволило оценить степень влияния особенностей наследования размера помета (ограниченность полом этого признака), а также наличие возрастной структуры в популяции на условия существования полиморфизма по рассматриваемому признаку. Оказалось, что изменение цикла кормовой базы может значительно изменять условия существования полиморфизма [51]. При этом реальная динамика жертвы может быть достаточно разнообразна, начиная от стационарной и строго периодической и заканчивая нестрогими (или зашумленными) циклами и даже нерегулярными колебаниями. Явное включение в модель популяционной динамики жертвы и рассмотрение полного сообщества, вместо локальной популяции, позволит избавиться от искусственного циклически изменяющегося параметра, вариация значений которого весьма ограничена, и оценить возможности поддержания полиморфизма в популяциях песца в более реалистичных условиях.

МОДЕЛЬ ДИНАМИКИ СООБЩЕСТВА “ХИЩНИК–ЖЕРТВА”, УЧИТЫВАЮЩАЯ ЕСТЕСТВЕННЫЙ ОТБОР В ПОПУЛЯЦИИ ХИЩНИКА

В качестве базовой модели для описания эволюционной динамики локальной популяции хищника рассмотрим классическую модель моногенного отбора по признаку, контролируемому одним аутосомным диаллельным локусом с аллеломорфами А и а в диплоидной популяции. Ограничимся случаем F-отбора, действие которого не зависит от численности (плотности населения) популяции хищника, однако при этом влияние плотностно-зависимых факторов, лимитирующих ее рост, учитывается на уровне общей популяционной численности. Обозначив через Y – численность популяции хищника, через p – частоту аллеля A в популяции хищника и через n – сезон размножения, можно получить следующие уравнения эволюционной динамики [52]:

(1)
$\left\{ {\begin{array}{*{20}{c}} {Y(n + 1) = \bar {w}(n)Y(n)f(Y(n))} \\ {p(n + 1) = {{p(n)({{w}_{{AA}}}p(n) + {{w}_{{Aa}}}(1 - p(n)))} \mathord{\left/ {\vphantom {{p(n)({{w}_{{AA}}}p(n) + {{w}_{{Aa}}}(1 - p(n)))} {\bar {w}(n).}}} \right. \kern-0em} {\bar {w}(n).}}} \end{array}} \right.$

Величина $\bar {w}(n)$ соответствует средней относительной приспособленности в n-ый сезон размножения и определяется следующим образом:

$\begin{gathered} \bar {w}(n) = {{w}_{{AA}}}p{{(n)}^{2}} + 2{{w}_{{Aa}}}p(n)(1 - p(n)) + \\ + \,\,{{w}_{{aa}}}{{(1 - p(n))}^{2}}, \\ \end{gathered} $
где wij – относительная приспособленность ij-го генотипа (индексы i, j могут принимать значения A, a), независящая от уровня численности.

Будем полагать, что при этом есть и плотностное лимитирование популяции, которое осуществляется по линейному закону одинаково для всех генотипов (дискретный аналог модели Ферхюльста): f(Yn) = 1 – Yn/М, где М – емкость экологической ниши хищника – максимально возможная его численность в сообществе.

Здесь важно отметить, что использование аналога модели Ферхюльста налагает существенные ограничения как на возможные (соответствующие биологическому смыслу задачи) значения параметров модели, так и на диапазоны рассматриваемых в модели численностей. В частности, предполагается, что численность хищника не может превышать величину М.

Для описания динамики локальной популяции жертвы также будем использовать дискретный аналог уравнения Ферхюльста:

(2)
$X(n + 1) = bX(n)\left( {1 - \frac{{X(n)}}{K}} \right),$
где X – численность жертвы в n-ый сезон размножения, b – ее репродуктивный потенциал, K – емкость экологической ниши жертвы. При этом предполагается, что численность жертвы не может превышать величину К.

Объединяя модели (1) и (2), будем использовать классические уравнения Лотки–Вольтерры с откликом в виде функции Холлинга II-го типа, учитывающей насыщение хищника. Кроме того, учтем генетическую неоднородность хищника, введя зависимость приспособленности генотипа (wij) от функции питания αij(Х) так, чтобы по аналогии с концепцией r-K отбора [53, 54] различные генотипы могли отличаться и по репродуктивному потенциалу (rij), и по функции питания αij(Х):

${{w}_{{ij}}}(X(n)) = {{r}_{{ij}}}{{\alpha }_{{ij}}}(X(n)),$
где rij – репродуктивный потенциал – максимально возможное значение коэффициента рождаемости и, соответственно, максимально возможное значение приспособленности ij-го генотипа, а

${{\alpha }_{{ij}}}(X(n)) = \frac{{X(n)}}{{{{C}_{{ij}}} + X(n)}}.$

Таким образом, функции питания различных генотипов отличаются только константой Cij, равной численности жертвы, при которой ij-ый генотип имеет приспособленность rij/2, и называемой константой полунасыщения хищника ij-ого генотипа. Учитывая все вышеизложенное, получаем:

(3)
$\left\{ {\begin{array}{*{20}{c}} {X(n + 1) = bX(n)\left( {1 - \frac{{X(n)}}{K}} \right) - \hat {\alpha }Y(n)\Psi (n)} \\ {Y(n + 1) = {{\bar {w}(n)Y(n)(1 - Y(n)} \mathord{\left/ {\vphantom {{\bar {w}(n)Y(n)(1 - Y(n)} M}} \right. \kern-0em} M})} \\ {p(n + 1) = p(n)({{w}_{{AA}}}(X(n))p(n) + {{{{w}_{{Aa}}}(X(n))(1 - p(n)))} \mathord{\left/ {\vphantom {{{{w}_{{Aa}}}(X(n))(1 - p(n)))} {\bar {w}(n)}}} \right. \kern-0em} {\bar {w}(n)}},} \end{array}} \right.$
где $\hat {\alpha }$ – среднее максимально возможное количество жертвы, потребляемое за один сезон одним хищником при его полном насыщении,
$\Psi (n) = X(n)\left( {\frac{{p{{{(n)}}^{2}}}}{{{{C}_{{AA}}} + X(n)}} + \frac{{2p(n)(1 - p(n))}}{{{{C}_{{Aa}}} + X(n)}} + \frac{{{{{(1 - p(n))}}^{2}}}}{{{{C}_{{aa}}} + X(n)}}} \right)$
– средневзвешенная по генетическому составу хищника доля (от максимально возможного количества) жертвы, потребляемая в данном сезоне одним хищником, учитывающая ограниченный размер популяции жертв, а также тот факт, что различные генотипические группы хищника оказывают неодинаковое давление на популяцию жертвы.

Отметим, что в случае генетически однородной популяции (например, мономорфной по аллелю А) Y = YAA = Yp2 уравнения динамики численности сообщества преобразуются к виду, эквивалентному классической модели хищник–жертва с плотностным лимитированием составляющих его популяций по модели Ферхюльста и насыщением хищника в виде функции Холлинга II типа [55]:

$\left\{ {\begin{array}{*{20}{c}} {Y(n + 1) = \frac{{{{r}_{{AA}}}X(n)}}{{{{C}_{{AA}}} + X(n)}}Y(n)({{1 - Y(n)} \mathord{\left/ {\vphantom {{1 - Y(n)} M}} \right. \kern-0em} M})} \\ {X(n + 1) = bX(n)\left( {1 - \frac{{X(n)}}{K}} \right) - \frac{{\hat {\alpha }X(n)Y(n)}}{{{{C}_{{AA}}} + X(n)}}.} \end{array}} \right.$

После перехода к относительным численностям (Х/K → x, Y/М → y) и соответствующим параметрам модели (Cij/K → cij, ${{\hat {\alpha }} \mathord{\left/ {\vphantom {{\hat {\alpha }} K}} \right. \kern-0em} K}$ → α) получим уравнения динамики сообщества в окончательном несколько упрощенном виде:

(4)
$\left\{ {\begin{array}{*{20}{c}} {x(n + 1) = bx(n)\left( {1 - x(n)} \right) - \alpha y(n)\psi (n)} \\ {y(n + 1) = \bar {w}(n)y(n)(1 - y(n))} \\ {p(n + 1) = p(n)({{w}_{{AA}}}(x(n))p(n) + {{w}_{{Aa}}}(x(n)){{(1 - p(n)))} \mathord{\left/ {\vphantom {{(1 - p(n)))} {\bar {w}(n).}}} \right. \kern-0em} {\bar {w}(n).}}} \end{array}} \right.$

Здесь все переменные x(n), у(n) и р(n) изменяются в пределах от 0 до 1,

${{w}_{{ij}}}(x(n)) = \frac{{{{r}_{{ij}}}x(n)}}{{{{c}_{{ij}}} + x(n)}}$ – функция приспособленности ij-ого генотипа хищника, $\bar {w}(n) = {{w}_{{AA}}}(x(n))p{{(n)}^{2}}$ + $2{{w}_{{Aa}}}(x(n))p(n)(1 - p(n))$ + + ${{w}_{{aa}}}(x(n)){{(1 - p(n))}^{2}}$ – средняя приспособленность популяции хищника,

$\psi (n) = x(n)\left( {\frac{{p{{{(n)}}^{2}}}}{{{{c}_{{AA}}} + x(n)}} + \frac{{2p(n)(1 - p(n))}}{{{{c}_{{Aa}}} + x(n)}} + \frac{{{{{(1 - p(n))}}^{2}}}}{{{{c}_{{aa}}} + x(n)}}} \right)$

– средневзвешенная по генетическому составу хищника доля (от максимально возможного количества) жертвы, потребляемая в данном сезоне одним хищником.

Полученная в результате эколого-генетическая модель (4) позволяет описать характерную особенность сообщества “песец–мышевидные грызуны”, в котором репродуктивный успех хищника зависит от обилия жертвы. Так, генотипы песца, производящие пометы большого размера, имеют большую плодовитость (больший репродуктивный потенциал rij), но для успешного выживания щенков им требуется больше пищи, т.е. константа полунасыщения для этих генотипов хищника (cij) тоже будет больше. Соответственно результирующая приспособленность генотипа хищника (wij) будет определяться совокупностью значений, характеризующих обилие жертвы и репродуктивные способности хищника.

Далее рассмотрим, как меняются приспособленности генотипов хищника в зависимости от численности жертвы при различных распределениях генетических характеристик хищника. Здесь мы ответим на вопрос, может ли меняться взаимное расположение приспособленностей генотипов, а следовательно и направление естественного отбора в популяции хищника при изменении численности жертвы.

Вариации вида зависимостей приспособленностей при изменении численности жертвы

Рассмотрим важные частные случаи зависимостей приспособленностей от численности популяции.

I. Константы полунасыщения хищников по генотипам не различаются (caa = cAa = cAA = с*).

В этом случае взаимное расположение репродуктивных потенциалов генотипов определяет взаимное расположение приспособленностей и не зависит от численности жертвы (рис. 1,а). Обозначим через g(x(n)) = x(n)/(c* + x(n)) характеристику пищевых ресурсов, тогда приспособленности можно представить в виде: wij(x(n)) = rijg(x(n)). Можно отметить, что в этом случае действует F‑отбор “в чистом виде”, так как относительные приспособленности генотипов постоянны.

Рис. 1.

Примеры зависимости изменений приспособленностей генотипов с ростом численности жертвы. а – постоянные относительные приспособленности (F-отбор): cAA = cAa = caa = 0.4, rAA = 1, raa = 2, rАa = 3; б – одинаковые репродуктивные потенциалы: rAA = rAa = raa = 2, cAA = 0.6, caa = 0.4, cАa = 0.2; в, г – изменение взаимного расположения приспособленностей с изменением численности жертвы: в – cAa = 0.45, caa = 0.3, cAA = 0.15, rAa = 2.5, raa = 2, rAA = 1.5; г – cAa = 0.6, caa = 0.4, cAA = 0.2, rAa = 4, raa = 2.5, rAA = 2.

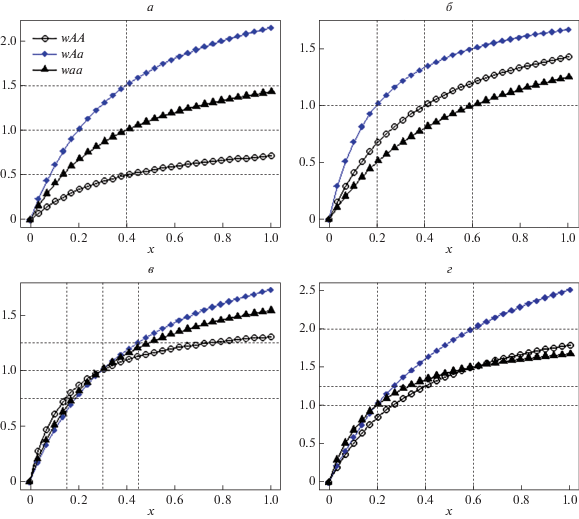
II. Репродуктивные потенциалы хищников с различными генотипами не отличаются (raa = rAa = = rAA = r).

В этом случае численность жертвы влияет на абсолютное значение приспособленности хищника, однако взаимное расположение приспособленностей не меняется, так как оно полностью определяется взаимным расположением констант полунасыщения хищника следующим образом: наиболее приспособленным генотипом оказывается генотип с наименьшим параметром cij: wij(x(n)) = r x(n)/(cij + + x(n)) (рис. 1,б).

III. Константы полунасыщения и репродуктивные потенциалы хищников различны.

Здесь возникают две принципиально различающиеся ситуации: в первом случае доминирование по репродуктивным потенциалам и константам полунасыщения у генотипов одинаковое (rAa > raa > rAA и cAa > caa > cAA), во втором – обратное (rAa > raa > rAA и cAa < caa < cAA). Отметим, что такой порядок (гетерозигота Аа на первом месте, гомозигота аа – на втором) выбран для примера, большинство возможных вариантов взаимного расположения приспособленностей можно получить, меняя только обозначения. Нетрудно показать, что во втором случае взаимное расположение приспособленностей определяется взаимным расположением их репродуктивных потенциалов и не меняется с изменением численности жертвы.

Другая ситуация (первый случай, когда rAa > raa > > rAA и cAa > caa > cAA) представляется наиболее реалистичной с биологической точки зрения, так как генотип с большим репродуктивным потенциалом скорее будет иметь и большую константу полунасыщения (как у песцов с большим размером помета), поскольку для выживания ему потребуется больше пищи. В этом случае направление отбора может зависеть от численности жертвы. На рис. 1,в приведен пример ситуации, когда при маленьких значениях численности жертвы в популяции хищника (x < 0.3) действует дизруптивный отбор (гетерозигота наименее приспособлена), а при бóльших (x > 0.3) – сверхдоминирование. Несколько другое соотношение репродуктивных потенциалов и констант полунасыщения генотипов хищника (рис. 1,г) создает ситуацию, в которой при маленьких значениях численности жертвы в популяции хищника (x < 0.2) действует направленный отбор против аллеля А (гетерозигота занимает промежуточное положение), а при бóльших (x > 0.2) возникает сверхдоминирование.

Здесь закономерно возникает вопрос к соотношению параметров генотипов (плодовитости (rij) и константы полунасыщения (cij)): какого преимущества достаточно генотипу для доминирования? Рассмотрим его на примере сверхдоминирования, пусть гетерозигота обладает наибольшей плодовитостью и соответственно наиболее требовательна к обилию пищевых ресурсов: (rAa > > raa > rAA и cAa > caa > cAA). Учитывая вид функций приспособленности, запишем:

$\begin{gathered} {{w}_{{Aa}}}(x) > {{w}_{{ii}}}(x) \Leftrightarrow \frac{{{{r}_{{Aa}}}x}}{{{{c}_{{Aa}}} + x}} > \frac{{{{r}_{{ii}}}x}}{{{{c}_{{ii}}} + x}} \Rightarrow \\ \Rightarrow \frac{{{{r}_{{Aa}}}}}{{{{r}_{{ii}}}}} > \frac{{{{c}_{{Aa}}} + x}}{{{{c}_{{ii}}} + x}}. \\ \end{gathered} $

Далее обозначим через mi преимущество по плодовитости гетерозиготы над соответствующей гомозиготой ii: ${{m}_{i}} = {{{{r}_{{Aa}}}} \mathord{\left/ {\vphantom {{{{r}_{{Aa}}}} {{{r}_{{ii}}}}}} \right. \kern-0em} {{{r}_{{ii}}}}},$ тогда условия доминирования можно записать в следующем виде:

$\begin{array}{*{20}{c}} {{{w}_{{Aa}}}(x) > {{w}_{{aa}}}(x) \Leftrightarrow {{c}_{{Aa}}} < {{m}_{a}}{{c}_{{aa}}} + x({{m}_{a}} - 1),} \\ {{{w}_{{Aa}}}(x) > {{w}_{{AA}}}(x) \Leftrightarrow {{c}_{{Aa}}} < {{m}_{A}}{{c}_{{AA}}} + x({{m}_{A}} - 1).} \end{array}\,\,\,\,\,(*)$

Таким образом, для безусловного доминирования генотипу с большей плодовитостью достаточно, чтобы его требования к обилию пищи вырастали в меньшее количество раз, чем имеющееся у него преимущество по плодовитости (${{{{c}_{{Aa}}}} \mathord{\left/ {\vphantom {{{{c}_{{Aa}}}} {{{c}_{{ii}}}}}} \right. \kern-0em} {{{c}_{{ii}}}}} < {{m}_{i}}$). Если это не выполняется, то при малых величинах численности жертвы приспособленность наиболее плодовитого генотипа будет меньше, чем у менее плодовитых, а при больших – больше. Значение численности жертвы (х), в котором меняется доминирование по приспособленностям из-за того, что обилие жертвы ниже его оказывается малым, а выше – достаточным, определяется из соотношений (*). Так, на рис. 1,в преимущество по плодовитости у гетерозиготы: ma = 1.25, mA = 5/3, но ее требования к обилию пищи превосходят эти значения (mi): ${{{{c}_{{Aa}}}} \mathord{\left/ {\vphantom {{{{c}_{{Aa}}}} {{{c}_{{aa}}}}}} \right. \kern-0em} {{{c}_{{aa}}}}} = 1.5 > 1.25$ и ${{{{c}_{{Aa}}}} \mathord{\left/ {\vphantom {{{{c}_{{Aa}}}} {{{c}_{{АА}}}}}} \right. \kern-0em} {{{c}_{{АА}}}}} = 3 > {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}.$ Мы видим, что при малых численностях жертвы гетерозигота уступает по приспособленности обеим гомозиготам. При больших значениях численности жертвы ситуация меняется. Из условий (*) можно получить численность жертвы (х > 0.3), при которой ограничения по пищевым ресурсам станут менее значимы, чем преимущество по плодовитости, и установится сверхдоминирование.

Возможные равновесия – стационарные точки модели и условия их устойчивости

При некотором достаточно большом наборе значений параметров и при определенных начальных условиях (начальных значениях переменных) все переменные модели (4) стремятся к конкретным равновесным значениям – стационарным точкам.

Обозначим через $\bar {x}$ – численность жертвы, $\bar {y}$ – численность хищника, а $\bar {p}$ – частоту аллеля А в стационарной точке, тогда приспособленности генотипов хищника в стационарной точке естественно обозначить как ${{\bar {w}}_{{ij}}} = {{w}_{{ij}}}(\bar {x}) = \frac{{{{r}_{{ij}}}\bar {x}}}{{{{c}_{{ij}}} + \bar {x}}}$ и среднюю приспособленность популяции хищника как $\bar {\bar {w}} = \bar {w}(\bar {x},\bar {p}) = {{\bar {w}}_{{AA}}}{{\bar {p}}^{2}}$ + $2{{\bar {w}}_{{Aa}}}\bar {p}(1 - \bar {p}) + {{\bar {w}}_{{aa}}}{{(1 - \bar {p})}^{2}}.$

Несмотря на сложность модели (4) и невозможность найти все ее равновесия аналитически, нам удалось получить классификацию ее стационарных точек, на основе анализа линеаризованной системы провести исследование их асимптотической устойчивости и сделать выводы о направлении эволюционной динамики сообщества для различных областей значений параметров модели. Так, при малом репродуктивном потенциале жертвы (b < 1) сообщество вырождается: $\bar {x} = 0,$ $\bar {y} = 0.$ При большем репродуктивном потенциале жертвы, но при малой равновесной средней приспособленности популяции хищника ($\bar {\bar {w}} < 1$) в сообществе остается только жертва, а хищник вымирает: $\bar {x} = 1 - {1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b},$ $\bar {y} = 0,$ причем если репродуктивный потенциал жертвы оказывается достаточно высок, то равновесие ее численности теряет устойчивость и происходят популяционные колебания жертвы, усложняющиеся с ростом репродуктивного потенциала.

Рассмотрим теперь параметрическую область модели, где существует полное сообщество, т.е. хищник не вымирает. Для этого необходимо наложить следующие ограничения на параметры модели: b > 1, $\bar {\bar {w}}$ > 1. В этой области модель (4) имеет три стационарные точки, принципиально различающиеся генетической структурой популяции хищника.

I. Мономорфизм по аллелю а: $\bar {p} = 0.$

Стационарная численность жертвы $\bar {x}$ является решением следующего уравнения:

$\begin{gathered} - b{{r}_{{aa}}}{{{\bar {x}}}^{3}} - {{r}_{{aa}}}(b{{c}_{{aa}}} - b + 1){{{\bar {x}}}^{2}} + \\ + \,\,(((b - 1){{c}_{{aa}}} - \alpha ){{r}_{{aa}}} + \alpha )\bar {x} + \alpha {{c}_{{aa}}} = 0, \\ \end{gathered} $

стационарная численность хищника: $\bar {y} = 1 - {1 \mathord{\left/ {\vphantom {1 {\bar {\bar {w}}}}} \right. \kern-0em} {\bar {\bar {w}}}}$ или $\bar {y} = \frac{{{{r}_{{aa}}}\bar {x} - {{c}_{{aa}}} - \bar {x}}}{{{{r}_{{aa}}}\bar {x}}}.$

Условия существования равновесия: b > 1, ${{\bar {w}}_{{aa}}} > 1;$ условия устойчивости мономорфизма ${{\bar {w}}_{{aa}}} > {{\bar {w}}_{{Aa}}}.$

II. Мономорфизм по аллелю А: $\bar {p} = 1.$

Стационарная численность жертвы $\bar {x}$ является решением следующего уравнения:

$\begin{gathered} - b{{r}_{{AA}}}{{{\bar {x}}}^{3}} - {{r}_{{AA}}}(b{{c}_{{AA}}} - b + 1){{{\bar {x}}}^{2}} + \\ + \,\,(((b - 1){{c}_{{AA}}} - \alpha ){{r}_{{AA}}} + \alpha )\bar {x} + \alpha {{c}_{{AA}}} = 0, \\ \end{gathered} $

стационарная численность хищника: $\bar {y} = 1 - {1 \mathord{\left/ {\vphantom {1 {\bar {\bar {w}}}}} \right. \kern-0em} {\bar {\bar {w}}}}$ или $\bar {y} = \frac{{{{r}_{{AA}}}\bar {x} - {{c}_{{AA}}} - \bar {x}}}{{{{r}_{{AA}}}\bar {x}}}.$

Условия существования данного равновесия: b > 1, ${{\bar {w}}_{{AA}}} > 1;$ условия устойчивости мономорфизма ${{\bar {w}}_{{AA}}} > {{\bar {w}}_{{Aa}}}.$

III. Полиморфизм: $\bar {p} = \frac{{{{{\bar {w}}}_{{Aa}}} - {{{\bar {w}}}_{{aa}}}}}{{2{{{\bar {w}}}_{{Aa}}} - {{{\bar {w}}}_{{aa}}} - {{{\bar {w}}}_{{AA}}}}}.$

Стационарная численность жертвы $\bar {x}$ в полиморфном равновесии является решением полиномиального уравнения 9-й степени, которое здесь мы не будем приводить из-за его громоздкости, стационарная численность хищника $\bar {y} = 1 - {1 \mathord{\left/ {\vphantom {1 {\bar {\bar {w}}}}} \right. \kern-0em} {\bar {\bar {w}}}},$ $\bar {\bar {w}} = \frac{{\bar {w}{{{_{{}}^{2}}}_{{Aa}}} - {{{\bar {w}}}_{{AA}}}{{{\bar {w}}}_{{aa}}}}}{{2{{{\bar {w}}}_{{Aa}}} - {{{\bar {w}}}_{{AA}}} - {{{\bar {w}}}_{{aa}}}}}.$ Условия его существования: b > 1, $\bar {\bar {w}} > 1;$ условия устойчивости полиморфизма ${{\bar {w}}_{{aa}}} < {{\bar {w}}_{{Aa}}}$ и ${{\bar {w}}_{{AA}}} < {{\bar {w}}_{{Aa}}}.$ Если обе гомозиготы более приспособлены, чем гетерозигота (${{\bar {w}}_{{aa}}} > {{\bar {w}}_{{Aa}}}$ и ${{\bar {w}}_{{AA}}} > {{\bar {w}}_{{Aa}}}$), то полиморфизм неустойчив и возникает бистабильность мономорфных состояний, в каком из них окажется популяция зависит от начальных условий.

Таким образом, направление эволюции популяции хищника, как и в более простых моделях, в целом определяется взаимным расположением приспособленностей его генотипов, при этом характер динамики определяется уже набором параметров, характеризующих репродуктивные способности жертвы и хищника, а также характеристиками межвидового взаимодействия.

Отметим, что приведенная выше классификация стационарных состояний корректна, когда численности популяций и, следовательно, приспособленности генотипов стабилизируются и их взаимное расположение не меняется. Если стабилизации численностей не происходит, то закономерно меняются и значения приспособленностей. В этом случае нужно рассматривать две принципиально различающиеся ситуации: (i) взаимное расположение приспособленностей не меняется (например, как на рис. 1,а, б) и результат отбора не меняют флуктуации численности – тогда классификация финитных состояний остается в силе; (ii) взаимное расположение приспособленностей меняется с изменением численности жертвы (например, как на рис. 1,в, г) и тогда в разных фазах динамики жертвы меняется направление отбора и его результат уже не так очевиден, здесь необходимо дополнительное численное исследование.

ДИНАМИКА СООБЩЕСТВА ПОД ДЕЙСТВИЕМ ЕСТЕСТВЕННОГО ОТБОРА В ПОПУЛЯЦИИ ХИЩНИКА

Прежде чем перейдем к анализу результатов действия естественного отбора в популяции хищника подчеркнем, что рассматривается параметрическая область, где существует полное сообщество, т.е. хищник не вымирает и выполняются следующие ограничения на параметры модели: b > 1, $\bar {w}$ > 1.2.

Численное исследование выполнено путем построения предельных траекторий модели (4) при заданных значениях параметров и начальных условий, также бифуркационных диаграмм и бассейнов притяжения ее альтернативных аттракторов.

Отметим, что в целом область устойчивого сосуществования видов охватывает значительную часть параметрического пространства и не имеет выраженной фрактальности, т.е. при адекватном выборе параметров (достаточном уровне воспроизводства в популяциях жертвы и хищника вне области их чрезмерно высоких значений) траектории модели (4) будут оставаться в области неотрицательных значений на протяжении всего периода расчетов (подробнее в Приложении).

Типы естественного отбора

Сначала рассмотрим ситуации, в которых направление отбора не меняется.

I. Промежуточное доминирование по приспособленностям (${{\bar {w}}_{{aa}}} > {{\bar {w}}_{{Aa}}} > {{\bar {w}}_{{AA}}}$).

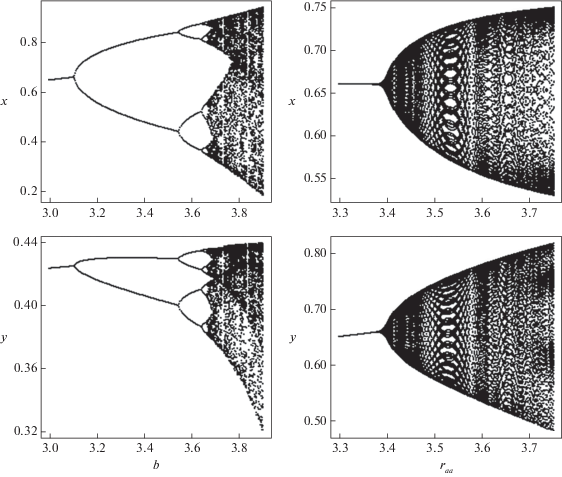
В этом случае полиморфного равновесия не существует, так как $\bar {p} = \frac{{{{{\bar {w}}}_{{Aa}}} - {{{\bar {w}}}_{{aa}}}}}{{2{{{\bar {w}}}_{{Aa}}} - {{{\bar {w}}}_{{aa}}} - {{{\bar {w}}}_{{AA}}}}}$ оказывается меньше нуля или больше единицы. Система (4) имеет только одно устойчивое мономорфное состояние ($\bar {p} = 0$), в котором и должна оказаться популяция хищника вне зависимости от начальных условий, т.е. происходит вытеснение неоптимального аллеля. При этом динамика численности сообщества зависит как от внутрипопуляционных параметров, так и от характеристик межпопуляционного взаимодействия. С ростом параметра b и ${{\bar {w}}_{{aa}}}$ решение ($\bar {p} = 0$) теряет устойчивость и численность популяций, составляющих сообщество, переходит в колебательный режим в результате реализации сценария Фейгенбаума (рис. 2, слева) или Неймарка-Сакера (рис. 2, справа). В частности, при высоком репродуктивном потенциале жертвы (b) и невысокой приспособленности хищника (waa) потеря устойчивости сопровождается появлением двугодичных колебаний и их последующим усложнением по сценарию Фейгенбаума (рис. 2, слева). Увеличение же приспособленности хищника (${{\bar {w}}_{{aa}}}$) за счет роста его репродуктивного потенциала (raa) при достаточно высоком уровне воспроизводства в популяции жертвы приводит к бифуркации Неймарка-Сакера и возникновению достаточно сложно организованных колебаний численности (квазипериодических режимов) (рис. 2, справа), не наблюдающихся в моделях локальных популяций без возрастной структуры [52, 56, 57].

Рис. 2.

Мономорфизм аа. Бифуркационная диаграмма численностей жертвы (x) и хищника (y) при фиксированных значениях параметров и начальных условиях: cAA = 0.1, cAa = 0.1, caa = 0.1, rAA = 0.95, rAa = 0.92, α = 0.1, x0 = 0.4, y0 = 0.2, p0 = 0.1; слева raa = 2.0, справа b = 3.25.

II. Сверхдоминирование ($\max ({{\bar {w}}_{{aa}}},{{\bar {w}}_{{AA}}}) < {{\bar {w}}_{{Aa}}}$) или повышенная приспособленность гетерозигот.

В этом случае оба мономорфных равновесия системы (4) неустойчивы и популяция остается полиморфной вне зависимости от начальных условий. При этом за счет отбора популяция хищника достигает большего значения средней приспособленности; динамика численности, как и при движущем отборе, определяется совокупностью внутрипопуляционных параметров и характеристик межпопуляционного взаимодействия. При сверхдоминировании увеличение репродуктивного потенциала жертвы или хищника может не только вызвать колебания численности сообщества, но и привести к возникновению устойчивых колебаний генетического состава хищника.

III. Пониженная приспособленность гетерозигот ($\min ({{\bar {w}}_{{aa}}},{{\bar {w}}_{{AA}}}) > {{\bar {w}}_{{Aa}}}$).

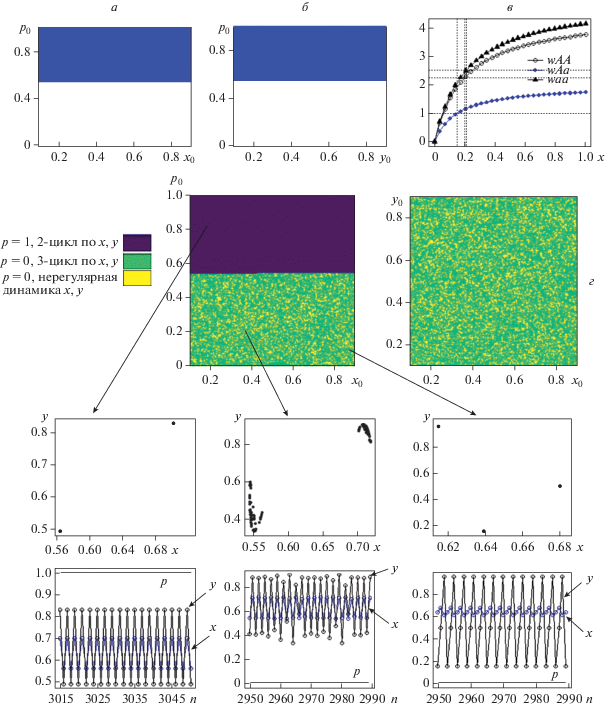
В этом случае оба мономорфных состояния модели (4) могут быть устойчивы, и система окажется в одном из них. От начальных условий зависит то, в каком именно из мономорфных равновесий окажется система (рис. 3). Причем зависимость от начальных условий выглядит предельно просто: при p0 < p* популяция достигнет генетически мономорфного состояния p = 0, при p0 > p* – p = 1, вне зависимости от начальных численностей сообщества (рис. 3). При этом динамика его численности определяется набором внутрипопуляционных параметров жертвы, хищника (точнее, эволюционно победившего хищника) и характеристик межвидового взаимодействия. Поэтому динамика численности сообщества с генетически различными хищниками может различаться (рис. 3,г). В частности, при выбранных значениях параметров в сообществе наблюдается мультистабильность, представленная тремя различными динамическими режимами численности хищника и жертвы: цикл длины 2 при мономорфизме АА у хищника, а также цикл длины 3 или нерегулярная динамика в случае фиксации аллеля а в популяции хищника. При этом бассейны притяжения различной динамики численности при мономорфизме аа у хищника создают очень сложную (фрактальную) структуру деления фазового пространства (рис. 3,г), поэтому переход от точного 3-цикла к нерегулярной динамике и наоборот может произойти в результате небольшого изменения текущей численности даже одного из видов сообщества.

Рис. 3.

а, б – бассейны притяжения мономорфных состояний модели (4): p = 1 – синим цветом, p = 0 – белым. Значения параметров и начальные условия: cAA = 0.2, cAa = 0.15, caa = 0.21, rAA = 4.5, rAa = 2.0, raa = 5.005, b = 3.0, α = 0.1, x0 = = 0.1, y0 = 0.8; p0 = 0.35 (а), p0 = 0.45 (б); в – динамика приспособленностей генотипов при изменении численности жертвы в диапазоне [0, 1]; г – бассейны притяжения различных динамических режимов модели (4). Темно-синим цветом обозначено мономорфное состояние p = 1, в котором реализуется 2-цикл по x, y (нижний ряд, слева), зеленым и желтым цветом – другое мономорфное состояние p = 0 с 3-циклом по x, y (нижний ряд, справа) и нерегулярной динамикой численностей популяций сообщества (нижний ряд, центр) соответственно.

Изменение типа естественного отбора в процессе эволюции сообщества

Рассмотрим ситуацию, когда направление отбора в популяции хищника зависит от доступности пищевых ресурсов, т.е. меняется с изменением численности жертвы. Причем генотип с большим репродуктивным потенциалом имеет большую константу полунасыщения (как у песцов с большим размером помета), поскольку для выживания ему требуется больше пищи. Пример такой ситуации представлен на рис. 4: при малых значениях численности жертвы (x < 0.5) отбор направлен против аллеля А, а при больших (x > 0.5) – против аллеля а, при этом приспособленность гетерозиготы занимает промежуточное положение, т.е. вне зависимости от численности жертвы в популяции хищника действует направленный отбор, но его направление может меняться в зависимости от доступности пищевых ресурсов (рис. 4,а).

Рис. 4.

Изменение типа естественного отбора. а – динамика приспособленностей генотипов при изменении численности жертвы в диапазоне [0, 1]. Значения параметров: cAA = 0.3, cAa = 0.2, caa = 0.1, rAA = 2.4, rAa = 2.1, raa = 1.8; б – бифуркационная диаграмма численности жертвы (х), хищника (у) и генетического состава хищника (p) с изменением репродуктивного потенциала жертвы (b) при фиксированных значениях параметров (α = 0.1, остальные совпадают с фрагментом (а)) и начальных условиях: x0 = 0.4, y0 = 0.1, p0 = 0.1; в – бассейны притяжения мономорфных равновесий модели при фиксированном значении параметра b = 2.1; y0 = 0.2 (слева), p0 = 0.1 (справа).

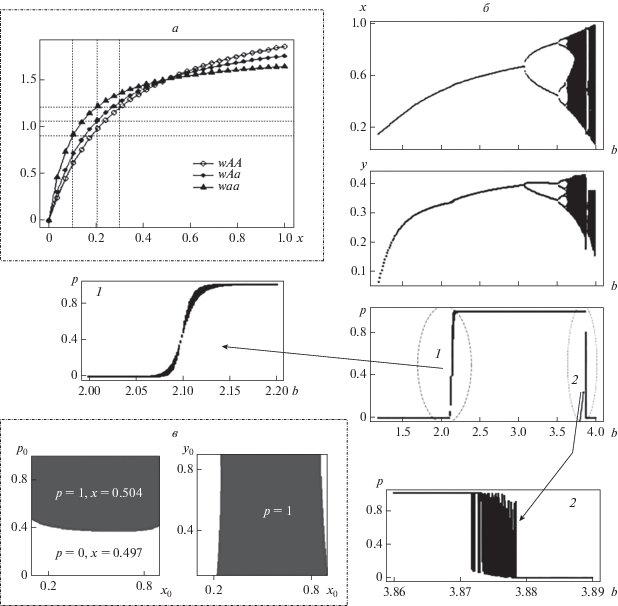
На бифуркационной диаграмме (рис. 4,б) пример эволюции сообщества в результате роста репродуктивного потенциала жертвы. Можно видеть, что при малых значениях бифуркационного параметра (b < 2.1) стационарная численность популяции жертвы оказывается небольшой ($\bar {x}$ < 0.5) и у хищника устанавливается мономорфизм аа. Рост репродуктивного потенциала жертвы (b) сначала приводит к увеличению ее стационарной численности, что при переходе через значение $\bar {x}$ = 0.5 (при b > 2.1) сопровождается изменением направления отбора в популяции хищника, который в результате оказывается мономорфным уже по другому аллелю (А). Этот переход характеризуется наличием области бистабильности (участок 1 бифуркационной диаграммы рис. 4,б, при b в небольшой окрестности значения 2.1), где результат отбора в популяции хищника зависит от начальных значений как генетического состава, так и численностей популяций, составляющих сообщество. В области бистабильности происходит очень медленное вытеснение одного из аллелей (вплоть до 30 000 поколений), поэтому на бифуркационной диаграмме можно видеть “след” переходного полиморфизма. Характерной чертой возникающей здесь бистабильности является то, что в каждом из мономорфных равновесий соответствующая гомозигота оказывается наиболее приспособленным генотипом из-за разницы в значениях стационарной численности жертвы ($\bar {x}$): ${{\left. {\bar {x}} \right|}_{{p = 0}}}$ < 0.5 и ${{\bar {w}}_{{aa}}} > {{\bar {w}}_{{Aa}}} > {{\bar {w}}_{{AA}}},$ a $\left. {{{{\bar {x}}}_{{p = 1}}}} \right|$ > 0.5 и ситуация меняется на обратную ${{\bar {w}}_{{aa}}} < {{\bar {w}}_{{Aa}}} < {{\bar {w}}_{{AA}}}.$ Отметим, что оба мономорфных равновесия здесь устойчивы, но оптимальным по приспособленности является равновесие p = 1, которое оказывается недостижимо из-за значительной области начальных значений. Пример бассейнов притяжения двух генетически различных состояний при фиксированном значении b = 2.1 приведен на рис. 4,в. Дальнейшее увеличение репродуктивного потенциала жертвы приводит к росту стационарных значений х и установлению мономорфизма АА в популяции хищника, вне зависимости от начальных условий. Еще большее увеличение бифуркационного параметра сопровождается потерей устойчивости мономорфного равновесия и возникновением колебаний численности популяций сообщества, при этом значительное увеличение амплитуды колебаний численности жертвы в результате реализации сложных нерегулярных режимов ее динамики создает условия для поддержания полиморфизма у хищника (участок 2 бифуркационной диаграммы рис. 4,б, при b между 3.87 и 3.88). Хотя внешне этот участок напоминает область бистабильности 1 (рис. 4,б), это уже не переходящий полиморфизм и он сохраняется вне зависимости от начальных условий (рис. 5). При этом колебания генетического состава представляют собой сумму двух колебательных процессов: короткопериодические колебания с маленькой амплитудой и длиннопериодический тренд с большой амплитудой. В результате в течение нескольких десятков поколений можно видеть популяцию хищника, почти достигшую мономорфного состояния аа или AA, но окончательного вытеснения редкого аллеля не происходит, эволюционный процесс меняет направление и способствует накоплению редкого аллеля с закономерным вытеснением генетического конкурента, пока он не потеряет количественное преимущество, а далее процесс опять поменяет направление на противоположное. Причем накопление аллеля А (с бóльшим репродуктивным потенциалом и соответственно бóльшими требованиями к обилию пищи) в популяции хищника происходит значительно медленнее, чем его вытеснение (рис. 5). Характер динамики жертвы (и хищника) визуально отличается при накоплении и вытеснении этого аллеля. Так, в течение относительно короткого (около 150 поколений) времени вытеснения аллеля А наблюдаются колебания численности жертвы в виде зашумленного 3-цикла с большой амплитудой и резким падением ее численности; более длительный процесс накопления этого аллеля (А) происходит на фоне нерегулярных колебаний численности жертвы, причем низкие значения ее численности (x < 0.5) в среднем встречаются реже, чем один раз в три года.

Рис. 5.

Полиморфизм хищника и смена динамического режима в популяции жертвы. Значения параметров совпадают с рис. 4,а. b = 3.876, x0 = 0.1, y0 = 0.2, p0 = 0.31.

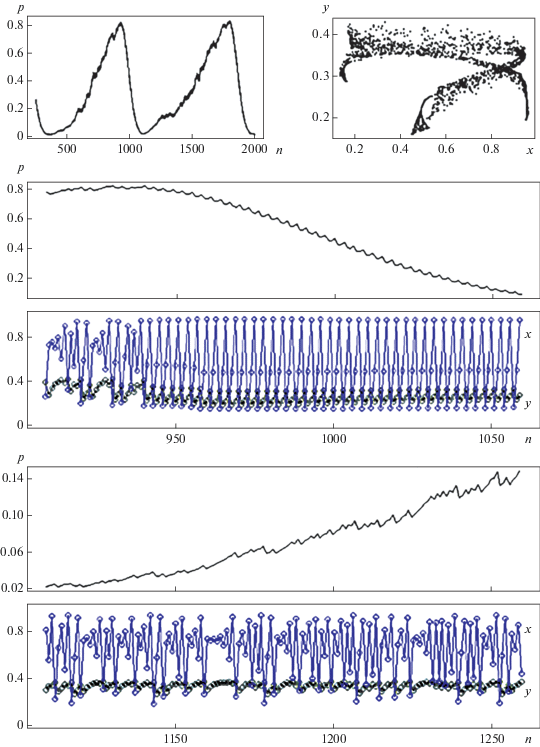
Возвращаясь к нашему модельному примеру – сообществу “песец–мышевидные грызуны”, отметим, что именно такой необычный тип полиморфизма, по-видимому, может поддерживаться в естественных популяциях континентальных песцов, поскольку в отсутствие сверхдоминирования (при рецессивном типе наследования больших пометов) значительные колебания численности мышевидных грызунов интенсивно меняют условия естественного отбора у своего хищника и в результате ни один из имеющихся аллелей не исчезает. В свою очередь, неодинаковое давление хищника на популяцию жертвы в разных фазах динамики его генетического состава может влиять уже на характер динамики самой жертвы. И это влияние может быть одной из причин наблюдаемой смены динамического режима в природных популяциях грызунов, сообщения о которых неоднократно появлялись в печати (например, [58, 59]).

ЗАКЛЮЧЕНИЕ

В работе предложена эколого-генетическая модель сообщества “хищник–жертва”, в которой приспособленность хищника определяется генетически одним диаллельным локусом. Полагается, что различные генотипы хищника, отличаясь по репродуктивному потенциалу, неодинаково приспособлены и к ограничению по пищевым ресурсам, т.е. приспособленности не являются постоянными, а функционально зависят от численности жертвы. Модель представлена уравнениями с дискретным временем, что позволяет учитывать ярко выраженную цикличность жизненного цикла видов, составляющих сообщество.

При моделировании воспроизводится ситуация, характерная для естественного сообщества “песец–мышевидные грызуны”, в котором мышевидные грызуны, являясь основной пищей для континентальных популяций песцов и обладая циклической динамикой численности, значительно влияют на репродуктивный уровень хищника. Причем эта важнейшая характеристика жизненного цикла песца определяется одним диаллельным локусом.

Проведено аналитическое и численное исследование предложенной модели. Показано, что направление эволюции популяции, как и в классической модели отбора по одному локусу с постоянными приспособленностями генотипов, определяется взаимным расположением приспособленностей генотипов хищника, при этом характер динамики определяется уже набором параметров, характеризующих репродуктивные способности жертвы и хищника, а также характеристиками межвидового взаимодействия. То есть при повышенной приспособленности гетерозиготы устанавливается полиморфизм, при промежуточной под действием направленного отбора происходит планомерное вытеснение неоптимального генотипа, а в случае пониженной приспособленности гетерозиготы наблюдается бистабильность двух мономорфных равновесий, в каждом из которых может оказаться популяция, в зависимости от начальных условий. Причем при нестационарной динамике жертвы (что весьма характерно для естественных популяций) область бистабильности в генетически различных мономорфных состояниях хищника характеризуется различной динамикой популяций, составляющих сообщество. При этом бассейны притяжения мономорфных равновесий обладают фрактальной структурой (рис. 3,г), т.е. небольшое изменение численности хищника или жертвы за счет случайных факторов может привести к закреплению другого аллеля в популяции хищника и смене динамического режима численности сообщества.

Возможность нарушения реализации классических эволюционных сценариев (приведенных выше) связана с тем, что приспособленности генотипов зависят от текущей численности жертвы, которая может стабилизироваться в стационарном состоянии или флуктуировать, не достигая его и изменяя значения приспособленностей различных генотипов хищника. И если хищник неоднороден по плодовитости и приспособленности к ограничению пищевых ресурсов, то в разных фазах динамики жертвы меняется направление отбора в популяции хищника. Таким образом, флуктуации обилия жертвы порождают разнонаправленный естественный отбор у хищника, при котором взаимное расположение приспособленностей его генотипов меняется. Здесь появляются радикально различающиеся сценарии эволюции хищника, обусловленные различными репродуктивными способностями жертвы (рис. 4, 5). Отметим, что этот эффект возникает в естественной ситуации, когда более плодовитые генотипы хищника более требовательны к обилию пищевых ресурсов (как у песцов). Так, при небольшом уровне воспроизводства в популяции жертвы происходит вытеснение гомозигот с бóльшим репродуктивным потенциалом и требованиями к пищевым ресурсам, что приводит к установлению мономорфизма; при бóльшем репродуктивном потенциале жертвы отбор идет уже против гомозигот, побеждавших в предыдущих условиях; а жертва с еще большей плодовитостью (приводящей к значительным флуктуациям ее популяционной численности) создает хищнику условия, в которых он сохраняет оба аллеля; для такого полиморфизма характерны долгие процессы вытеснения и накопления аллелей, не приводящие к полной потере ни одного из них, и значительно отличающаяся визуально динамика численности в разных фазах этого процесса, что может распознаваться наблюдателем как смена динамического режима в популяции любого из видов сообщества. При этом приспособленность гетерозиготы занимает промежуточное положение, т.е. при больших и малых численностях жертвы максимальными являются приспособленности противоположных гомозигот, и в рамках классической теории естественного отбора установление полиморфизма при таких условиях было бы невозможно.

Отметим, что подобный флуктуирующий полиморфизм может существовать в естественных популяциях континентальных песцов, поскольку в отсутствие сверхдоминирования (из-за рецессивного типа наследования пометов большого размера у песца) значительные колебания численности мышевидных грызунов, являющихся их основным пищевым ресурсом, интенсивно меняют условия естественного отбора для своего хищника и в результате ни один из имеющихся аллелей не исчезает. В свою очередь, неодинаковое давление хищника на популяцию жертвы в разных фазах динамики его генетического состава может влиять уже на характер динамики самой жертвы. И это влияние может быть одной из причин наблюдаемой смены динамического режима в природных популяциях грызунов, сообщения о которых неоднократно появлялись в печати, например изменение цикла в популяциях лемминга Lemmus lemmus на юге Норвегии [59] и красно-серой полeвки Clethrionomys rufocanus, обитающей в Финляндии [58].

Работа выполнена в рамках государственных заданий Института автоматики и процессов управления ДВО РАН, Института комплексного анализа региональных проблем ДВО РАН.

Настоящая статья не содержит каких-либо исследований с использованием в качестве объекта животных.

Настоящая статья не содержит каких-либо исследований с участием в качестве объекта людей.

Авторы заявляют, что у них нет конфликта интересов.

Список литературы

  1. Lotka A.J. Elements of Physical Biology. Baltimore: Williams and Wilkins, 1925. 460 p.

  2. Volterra V. Leçons sur la théorie mathématique de la lutte pour la vie. Paris: Gauthiers–Villars, 1931. 214 p.

  3. Базыкин А.Д. Математическая биофизика взаимодействующих популяций. М.: Наука, 1985. 181 с.

  4. Базыкин А.Д. Нелинейная динамика взаимодействующих популяций. М.; Ижевск: Ин-т компьют. исслед., 2003. 368 с.

  5. Kingsland S.E. Modeling Nature: Episodes in the History of Population Ecology. 2nd ed. Chicago: Univ. Chicago Press, 1995. 306 p.

  6. Kingsland S. Alfred J. Lotka and the origins of theoretical population ecology // Proc. Natl Acad. Sci. USA. 2015. V. 112. №. 31. P. 9493–9495.

  7. Фрисман Е.Я., Кулаков М.П., Ревуцкая О.Л. и др. Основные направления и обзор современного состояния исследований динамики структурированных и взаимодействующих популяций // Компьютерные исследования и моделирование. 2019. Т. 11. № 1. С. 119–151.

  8. Morozov A. Mathematical modelling in theoretical ecology: introduction to the special issue // Mathem. Modelling of Natural Phenomena. 2013. V. 8. № 6. P. 1–4.

  9. Malthus T.R. An Essay on the Principle of Population. London, UK: J. Johnson, 1798. 432 p.

  10. Verhulst P.F. Notice sur la loi que la population suit dans son accroissement // Corresp. Math. Phys. 1838. V. 10. P. 113–126.

  11. Kostitzin V.A. Biologie mathématique. Paris: Librairie Armand Colin, 1937. 223 p.

  12. Pimentel D. Animal population regulation by the genetic feed-back mechanism // American Naturalist. 1961. V. 95. P. 65–79.

  13. Pimentel D. Population regulation and genetic feedback // Science. 1968. V. 159. P. 1432–1437.

  14. Levin S.A., Udovic J.D. A mathematical model of coevolving populations // Am. Naturalist. 1977. V. 111. P. 657–675.

  15. Schaffer W.M., Rosenzweig M.L. Homage to the Red Queen. I. Coevolution of predators and their victims // Theor. Popul. Biol. 1978. V. 14. P. 135–157.

  16. Fischer R.A. The Genetical Theory of Natural Selection. Oxford: Clarendon Press, 1930. 360 p.

  17. Haldane J.B.S., Jayakar S.D. Polymorphism due to selection of varying direction // J. Genetics. 1963. V. 58. № 2. P. 237–242.

  18. Wright S. Evolution in Mendelian populations // Genetics. 1930. V. 16. P. 97–159.

  19. Carroll S.P., Hendry A.P., Reznick D.N., Fox C.W. Evolution on ecological time-scales // Func. Ecol. 2007. V. 21. № 3. P. 387–393.

  20. Fussmann G.F., Loreau M., Abrams P.A. Eco-evolutionary dynamics of communities and ecosystems // Functional Ecology. 2007. V. 21. № 3. P. 465–477.

  21. Yamamichi M. Effects of rapid evolution on population cycles and extinction in predator–prey systems // Diversity of Functional Traits and Interactions. Theoretical Biology / Eds Mougi A. Singapore: Springer, 2020. https://doi.org/10.1007/978-981-15-7953-0_2

  22. Thompson J.N. Rapid evolution as an ecological process // Trends Ecol. Evol. 1998. V. 13. P. 329–332.

  23. Duffy M.A., Sivars-Becker L. Rapid evolution and ecological host-parasite dynamics // Ecol. Lett. 2007. V. 10. P. 44–53.

  24. Ellner S.P., Geber M.A., Hairston N.G. Does rapid evolution matter? Measuring the rate of contemporary evolution and its impacts on ecological dynamics // Ecol. Lett. 2011. V. 14. P. 603–614.

  25. Yoshida T., Jones L.E., Ellner S.P. et al. Rapid evolution drives ecological dynamics in a predator-prey system // Nature. 2003. V. 424. P. 303–306.

  26. Гинзбург Э.Х. Описание наследования количественных признаков. Новосибирск: Наука, 1984. 250 с.

  27. Abrams P.A., Matsuda H. Prey adaptation as a cause of predator-prey cycles // Evolution. 1997. V. 51. № 6. P. 1742–1750.

  28. Morozov A.Yu., Pasternak A.F., Arashkevich E.G. Revisiting the role of individual variability in population persistence and stability // PLoS One. 2013. V. 8. № 8. e70576. https://doi.org/10.1371/journal.pone.0070576

  29. Farkas J.Z., Morozov A.Y. Modelling effects of rapid evolution on persistence and stability in structured predator-prey systems // Mathem. Modelling of Natural Phenomena. 2014. V. 9. № 3. P. 26–46.

  30. Cortez M.H., Weitz J.S. Coevolution can reverse predator–prey cycles // Proc. Natl Acad. Sci. USA. 2014. V. 111. № 20. P. 7486–7491.

  31. Букин Ю.С. Процессы коэволюции в системе “хищник–жертва”. Эколого-генетическая модель // Вавил. журн. генетики и селекции. 2015. Т. 18. № 2. С. 320–328.

  32. Mougi A. Rapid evolution of prey maintains predator diversity // PLoS One. 2019. V. 14. № 12. e0227111. https://doi.org/10.1371/journal

  33. Venturino E. An ecogenetic model // Appl. Math. Lett. 2012. V. 25. P. 1230–1233.

  34. Viberti C., Venturino E. An ecosystem with HTII response and predators’ genetic variability // Math. Model. Anal. 2014. V. 19. P. 371–394.

  35. Rahman M.D. Modelling of an eco-genetic system: A mathematical model // Int. J. Ecol. Econ. Stat. 2016. V. 37. P. 102–119.

  36. Castellino L., Peretti S., Rivoira S., Venturino E. A mathematical ecogenetic predator-prey model where both populations are genetically distinguishable // AIP Conf. Proc. 2016. V. 1776. 020006.

  37. Azzali I., Marcaccio G., Turrisi R., Venturino E. A genetically distinguishable competition model // Modern Mathematical Methods and High Performance Computing in Science and Technology / Eds Singh V. et al. Singapore: Springer. 2016. V. 171. P. 129–140.

  38. Wang L., Zhao J. A predator-prey model with genetic differentiation both in the predator and prey // Mathem. Biosciences and Engineering. 2020. V. 17. № 3. P. 2616–2635.

  39. Tyutyunov Yu., Zhadanovskaya E., Bourguet D., Arditi R. Landscape refuges delay resistance of the European corn borer to Bt-maize: A demogenetic dynamic model // Theoret. Population Biology. 2008. V. 74. № 1. P. 138–146.

  40. Tyutyunov Y.V., Kovalev O.V., Titova L.I. Spatial demogenetic model for studying phenomena observed upon introduction of the ragweed leaf beetle in the South of Russia // Mathem. Modelling of Natural Phenomena. 2013. V. 8. № 6. P. 80–95.

  41. Титова Л.И., Тютюнов Ю.В., Ковалёв О.В. Демогенетическая модель естественного отбора признаков, определяющих подвижность животных // Математическое моделирование в экологии: Материалы Пятой Национальной науч. конф. с межд. участием. Пущино. 2017. С. 223–224.

  42. Axenovich T.I., Zorkoltseva I.V., Akberdin I.R. et al. Inheritance of litter size at birth in farmed arctic foxes (Alopex lagopus, Canidae, Carnivora) // Heredity. 2007. V. 98. P. 99–105.

  43. Володин И.А., Калашникова М.В., Клинкова Е.С. и др. Структура поселения песца Alopex lagopus beringensis на северной оконечности острова Беринга // Зоол. журн. 2012. Т. 91. № 10. С. 1231–1236.

  44. Hersteinsson P., Macdonald D.W. Diet of Arctic foxes (Alopex lagopus) in Iceland // J. Zool. 1996. V. 240. P. 457–474.

  45. Angerbjörn A., Tannerfeldt M., Erlinge S. Predator-prey relationships: Arctic foxes and lemmings // J. Anim. Ecol. 1999. V. 68. P. 34–49.

  46. Tannerfeldt M., Angerbjörn A. Fluctuating resources and the evolution of litter size in the arctic fox // Oikos. 1998. V. 83. P. 545–559.

  47. Tannerfeldt M., Angerbjörn A. Life history strategies in a fluctuating environment: establishment and reproductive success in the arctic fox // Ecography. 1998. V. 19. P. 209–220.

  48. Elmhagen B., Tannerfeldt M., Verucci P., Angerbjörn A. The arctic fox (Alopex lagopus) – an opportunistic specialist // J. Zool. 2000. V. 251. P. 139–149.

  49. Жданова О.Л., Фрисман Е.Я. Математическое моделирование механизма дифференциации репродуктивных стратегий в естественных популяциях (на примере песцов, Alopex lagopus) // Компьютерные исследования и моделирование. 2016. Т. 8. № 2. С. 213−228.

  50. Жданова О.Л., Фрисман Е.Я. Математическое моделирование отбора по ограниченному полом признаку: к вопросу о существовании полиморфизма по размеру помета в естественных популяциях песцов // Генетика. 2021. Т. 57. № 2. С. 229–240. https://doi.org/10.31857/S0016675821020156

  51. Zhdanova O.L., Frisman E.Ya. Genetic polymorphism under cyclical selection in long-lived species: the complex effect of age structure and maternal selection // J. Theoret. Biology. 2021. V. 512. 110564. https://doi.org/10.1016/j.jtbi.2020.110564

  52. Фрисман Е.Я., Жданова О.Л., Неверова Г.П. Эколого-генетические модели в популяционной биофизике // Биофизика. 2020. Т. 65. № 5. С. 949–966. https://doi.org/10.31857/S0006302920050130

  53. Charlesworth B. Selection in density-regulated populations // Ecology. 1971. V. 52. P. 469−474.

  54. Rougharden J. Density dependent natural selection // Ecology. 1971. V. 52. P. 453−468.

  55. Неверова Г.П., Жданова О.Л., Абакумов А.И. Дискретная модель сезонного цветения планктона // Математ. биология и биоинформатика. 2020. № 2. С. 235–250. https://doi.org/10.17537/2020.15.235

  56. Жданова О.Л., Фрисман Е.Я. Проявление мультирежимности в простейшей эколого-генетической модели эволюции популяций // Генетика. 2016. Т. 52. № 8. С. 975–984.

  57. Zhdanova O.L., Frisman E.Ya. Alternative attractors in an ecological-genetic model of populations with non-overlapping generations // Ecol. Complexity. 2017. V. 31. P. 135–143. https://doi.org/10.1016/j.ecocom.2017.06.009

  58. Henttonen H., Wallgren H. Small rodent dynamics and communities in the birch forest zone of northern Fennoscandia // Nordic Mountain Birch Ecosystems / Ed. Wielgolaski F.E. N.Y.: Parthenon, 2001. P. 262–278.

  59. Kausrud K.L., Mysterud A., Steen H. et al. Linking climate change to lemming cycles // Nature. 2008. V. 456. P. 93–97.

Дополнительные материалы

скачать ESM.doc
Приложение 1.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Генетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал